Calcul de l'élément chauffant

Pour déterminer l'un des principaux paramètres du fil de l'élément chauffant - diamètre d, m (mm), deux méthodes de calcul sont utilisées: en fonction de la puissance surfacique spécifique admissible PF et en utilisant le tableau des charges de courant.

Puissance surfacique spécifique admissible PF= P⁄F,

où P est la puissance du fil chauffant, W;

F = π ∙ d ∙ l — surface du réchauffeur, m2 ; l — longueur du fil, m.

Selon la première méthode

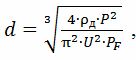
où ρd — résistance électrique du matériau du fil à la température réelle, Ohm • m ; U est la tension du fil chauffant, V ; PF - valeurs admissibles de puissance de surface spécifique pour différents appareils de chauffage :

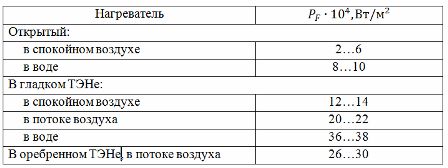
La deuxième méthode utilise un tableau des charges de courant (voir tableau 1) compilé à partir de données expérimentales. Pour utiliser le tableau indiqué, il est nécessaire de déterminer la température de chauffage calculée Tp par rapport à la température réelle (ou admissible) du conducteur Td par le rapport :

Tr = Km ∙ Ks ∙ Td,

où Km est le facteur d'installation, en tenant compte de la détérioration des conditions de refroidissement de l'aérotherme due à sa construction ; Kc est le facteur ambiant, compte tenu de l'amélioration des conditions de refroidissement du réchauffeur par rapport à un environnement d'air stationnaire.

Pour un élément chauffant en fil torsadé en spirale, Km = 0,8 … 0,9 ; idem, avec une base en céramique Km = 0,6 ... 0,7; pour un fil de plaques chauffantes et certains éléments chauffants Km = 0,5 ... 0,6; pour un conducteur d'un plancher électrique, sol et éléments chauffants Km = 0,3 ... 0,4. Une plus petite valeur de Km correspond à un réchauffeur de plus petit diamètre, une plus grande valeur à un plus grand diamètre.

En cas de fonctionnement dans des conditions autres que la convection libre, Kc = 1,3 … 2,0 est pris pour les éléments chauffants dans le flux d'air ; pour les éléments en eau calme Kc = 2,5 ; dans le débit d'eau — Kc = 3,0 … 3,5.

Si la tension Uph et la puissance Pf du futur réchauffeur (conçu) sont définies, alors son courant (par phase)

Iph = Pph⁄Uph

Selon la valeur calculée du courant de l'appareil de chauffage pour la température calculée nécessaire de son chauffage selon le tableau 1, le diamètre requis du fil de nichrome d est trouvé et la longueur requise du fil, m, pour la fabrication de l'appareil de chauffage est calculé:

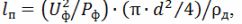
où d est le diamètre de fil sélectionné, m ; ρd est la résistance électrique spécifique du conducteur à la température de chauffage réelle, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

où αр — coefficient de température de résistance, 1/OS.

Pour déterminer les paramètres de la spirale nichrome, prenons le diamètre moyen des spires D = (6 … 10) ∙ d, le pas de la spirale h = (2 … 4) ∙ d,

nombre de tours

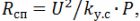
longueur d'hélice lsp = h ∙ n.

Lors du calcul des éléments chauffants, il convient de rappeler que la résistance du fil en spirale après avoir appuyé sur l'élément chauffant

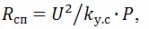
où k (y.s) est un coefficient qui tient compte de la diminution de la résistance de la spirale ; selon les données expérimentales, k (s) = 1,25. Il convient également de tenir compte du fait que la puissance de surface spécifique du fil en spirale est 3,5 à 5 fois supérieure à la puissance de surface spécifique de l'élément chauffant tubulaire.

Dans les calculs pratiques de l'élément chauffant, déterminez d'abord la température de sa surface Tp = To + P ∙ Rt1,

où It est la température ambiante, ° C; P est la puissance de l'élément chauffant, W; RT1 — résistance thermique à l'interface tuyau — milieu, ОC / W.

Ensuite, la température de l'enroulement est déterminée : Tsp = À + P ∙ (Rt1 + Rt2 + Rt3),

où Rt2 est la résistance thermique de la paroi du tuyau, ОC / W ; RT3 - résistance thermique de la charge, ОC / W; Rp1 = 1⁄ (α ∙ F), où α est le coefficient de transfert de chaleur, W / (m ^ 2 • ОС) ; F - surface de l'appareil de chauffage, m2; Rt2 = δ⁄ (λ ∙ F), où δ est l'épaisseur de paroi, m ; λ — conductivité thermique du mur, W / (m • ОС).

Pour plus d'informations sur le dispositif des éléments chauffants, voir ici : Éléments chauffants. Appareil, sélection, fonctionnement, raccordement des éléments chauffants

Tableau 1. Tableau des charges de courant

Exemple 1. Calculer le réchauffeur électrique sous la forme d'une spirale de fil en fonction de la puissance surfacique spécifique admissible PF.

Condition.Puissance de chauffage P = 3,5 kW ; tension d'alimentation U = 220 V ; matériau du fil - nichrome Х20Н80 (un alliage de 20% de chrome et 80% de nickel), donc la résistance électrique spécifique du fil ρ20 = 1,1 ∙ 10 ^ ( - 6) Ohm • m; coefficient de température de résistance αр = 16 ∙ 10 ^ (- 6) 1 /ОС; la spirale est ouverte, sous forme métallique, la température de fonctionnement de la spirale est Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Déterminer d, lp, D, h, n, lp.

Répondre. Résistance de la bobine : R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohms.

Résistance électrique spécifique à Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Trouver le diamètre du fil :

De l'expression R = (ρ ∙ l) ⁄S on obtient l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), d'où la longueur du fil

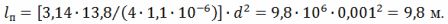
Le diamètre moyen du tour en spirale est D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Pas de spirale h = 3 ∙ d = 3 ∙ 1 = 3 mm.

Le nombre de tours de la spirale

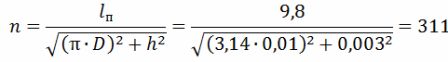
La longueur de l'hélice est lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Exemple 2. Calculez structurellement la résistance chauffante du fil lors de la détermination du diamètre du fil d à l'aide du tableau des charges de courant (voir tableau 1).

Condition. Puissance du fil chauffant P = 3146 W ; tension d'alimentation U = 220 V ; matériau du fil — nichrome Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃ ; hélice ouverte située dans le flux d'air (Km = 0,85, Kc = 2,0) ; température de fonctionnement admissible du conducteur Td = 470 ОС.

Déterminer le diamètre d et la longueur du fil lp.

Répondre.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

Le courant de chauffage de conception I = P⁄U = 3146⁄220 = 14,3 A.

Selon le tableau des charges de courant (voir tableau 1) à Tр = 800 ОС et I = 14,3 A, on trouve le diamètre et la section du fil d = 1,0 mm et S = ​​0,785 mm2.

Longueur de fil lp = (R ∙ S) ⁄ρ800,

où R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ] = 1,11 ∙ 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Aussi, si nécessaire, comme dans le premier exemple, D, h, n, lsp peuvent être définis.

Exemple 3. Déterminer la tension admissible du réchauffeur électrique tubulaire (TEN).

Condition... La bobine de l'élément chauffant est en fil de nichrome de diamètre d = 0,28 mm et de longueur l = 4,7 m L'élément chauffant est dans de l'air calme à une température de 20 °C. Caractéristiques du nichrome : ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m ; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. La longueur de la partie active du boîtier de l'élément chauffant est La = 40 cm.

L'élément chauffant est lisse, diamètre extérieur dob = 16 mm. Coefficient de transfert de chaleur α = 40 W / (m ^ 2 ∙ ° C). Résistances thermiques : remplissage RT3 = 0,3 ОС / W, parois du boîtier Rт2 = 0,002 ОС / W.

Déterminez quelle tension maximale peut être appliquée à l'élément chauffant afin que sa température de bobine Tsp ne dépasse pas 1000 ℃.

Répondre. Température de l'élément chauffant de l'élément chauffant

Tsp = À + P ∙ (Rt1 + Rt2 + Rt3),

où It est la température de l'air ambiant; P est la puissance de l'élément chauffant, W; RT1 — résistance thermique de contact de l'interface tuyau-milieu.

Puissance de l'élément chauffant P = U ^ 2⁄R,

où R est la résistance du serpentin de chauffage.On peut donc écrire Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), d'où la tension sur l'élément chauffant

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Trouver R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

où ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1,12 ∙ 10 ^ ( — 6) Ohm • m.

Alors R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Contacter la résistance thermique RT1 = 1⁄ (α ∙ F),

où F est l'aire de la partie active de la coque de l'élément chauffant; F = π ∙ db ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Trouvez Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Déterminez la tension de l'élément chauffant U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Si la tension nominale indiquée sur l'élément chauffant est de 220 V, alors la surtension à Tsp = 1000 OS sera de 5,6 % ∙ Un.