Batteries. Exemples de calcul
 Les batteries sont des sources de courant électrochimique qui, après décharge, peuvent être chargées à l'aide d'un courant électrique tiré d'un chargeur. Lorsque le courant de charge circule dans la batterie, une électrolyse se produit, à la suite de quoi des composés chimiques se forment sur l'anode et la cathode qui se trouvaient sur les électrodes dans l'état de fonctionnement initial de la batterie.
Les batteries sont des sources de courant électrochimique qui, après décharge, peuvent être chargées à l'aide d'un courant électrique tiré d'un chargeur. Lorsque le courant de charge circule dans la batterie, une électrolyse se produit, à la suite de quoi des composés chimiques se forment sur l'anode et la cathode qui se trouvaient sur les électrodes dans l'état de fonctionnement initial de la batterie.
L'énergie électrique, lorsqu'elle est chargée dans une batterie, est convertie en une forme chimique d'énergie. Lorsqu'elle est déchargée, la forme chimique de l'énergie devient électrique. Il faut plus d'énergie pour charger une batterie que ce qui peut être obtenu en la déchargeant.
La tension de chaque cellule d'une batterie au plomb après une charge de 2,7 V ne doit pas descendre en dessous de 1,83 V lors de la décharge.
La tension moyenne d'une batterie nickel-fer est de 1,1 V.
Les courants de charge et de décharge de la batterie sont limités et fixés par le constructeur (environ 1 A pour 1 dm2 de plaque).
La quantité d'électricité qui peut être tirée d'une batterie chargée est appelée la capacité en ampères-heure de la batterie.
Les batteries se caractérisent également par leur efficacité énergétique et de courant.Le retour d'énergie est égal au rapport de l'énergie reçue lors de la décharge sur l'énergie dépensée pour charger la batterie : ηen = Araz / Azar.
Pour une batterie plomb-acide ηen = 70% et pour une batterie fer-nickel ηen = 50%.
Le courant de sortie est égal au rapport entre la quantité d'électricité reçue lors de la décharge et la quantité d'électricité consommée lors de la charge : ηt = Q fois / Qchar.
Les batteries plomb-acide ont ηt = 90% et les batteries fer-nickel ηt = 70%.
Calcul de la batterie
1. Pourquoi le retour de courant de la batterie est-il supérieur au retour d'énergie ?
ηen = Araz / Azar = (Up ∙ Ip ∙ tp) / (Uz ∙ Iz ∙ tz) = Up / Uz ∙ ηt.
Le retour d'énergie est égal au retour de courant ηt multiplié par le rapport de la tension de décharge à la tension de charge. Puisque le rapport Uр / U3 <1, alors ηen <ηt.
2. Une batterie au plomb avec une tension de 4 V et une capacité de 14 Ah est illustrée à la fig. 1. La connexion des plaques est illustrée à la fig. 2. La connexion des plaques en parallèle augmente la capacité de la batterie. Deux ensembles de plaques sont connectés en série pour augmenter la tension.
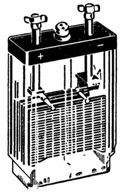
Riz. 1. Batterie au plomb
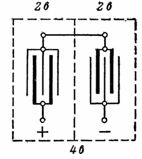
Riz. 2. Connexion des plaques d'une batterie au plomb pour une tension de 4 V
La batterie se charge en 10 heures avec un courant Ic = 1,5 A et se décharge en 20 heures avec un courant Ip = 0,7 A. Quel est le rendement en courant ?
Qp = Ip ∙ tp = 0,7 ∙ 20 = 14 UNE • h ; Qz = Iz ∙ tz = 1,5 ∙ 10 = 15 A • h; ηt = Qp / Qz = 14/15 = 0,933 = 93 %.
3. La batterie est chargée avec un courant de 0,7 A pendant 5 heures. Combien de temps se déchargera-t-il avec un courant de 0,3 A avec une sortie courant ηt = 0,9 (Fig. 3) ?
Riz. 3. Figure et schéma de l'exemple 3
La quantité d'électricité utilisée pour charger la batterie est : Qz = Iz ∙ tz = 0,7 ∙ 5 = 3,5 A • h.
La quantité d'électricité Qp libérée lors de la décharge est calculée par la formule ηt = Qp / Qz, d'où Qp = ηt ∙ Qz = 0,9 ∙ 3,5 = 3,15 A • h.
Temps de décharge tp = Qp / Ip = 3,15 / 0,3 = 10,5 heures.
4. La batterie de 20 Ah a été complètement chargée en 10 heures à partir du secteur via un redresseur au sélénium (Fig. 4). La borne positive du redresseur est connectée à la borne positive de la batterie lors de la charge. Avec quel courant la batterie est-elle chargée si le rendement en courant ηt = 90 % ? Avec quel courant la batterie peut-elle être déchargée en 20 heures ?
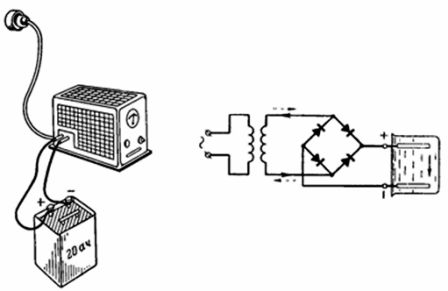
Riz. 4. Figure et schéma de l'exemple 4
Le courant de charge de la batterie est : Ic = Q / (ηt ∙ tc) = 20 / (10 ∙ 0,9) = 2,22 A. Courant de décharge admissible Iр = Q / tr = 20/20 = 1 A.
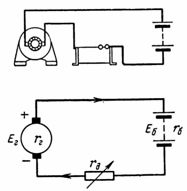
5. Une batterie d'accumulateurs composée de 50 cellules est chargée avec un courant de 5 A. une cellule de batterie 2,1 V et sa résistance interne rvn = 0,005 Ohm. Quelle est la tension de la batterie ? Qu'est-ce que etc. c. doit avoir un générateur de charge avec une résistance interne rg = 0,1 Ohm (Fig. 5) ?
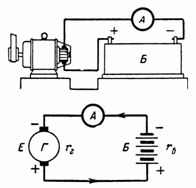
Riz. 5. Figure et schéma de l'exemple 5
La batterie D. d. C. est égale à : Eb = 50 ∙ 2,1 = 105 V.
Résistance interne de la batterie rb = 50 ∙ 0,005 = 0,25 Ohm. Le générateur D. d. S. est égal à la somme de e. etc. avec batteries et chute de tension dans la batterie et le générateur : E = U + I ∙ rb + I ∙ rg = 105 + 5 ∙ 0,25 + 5 ∙ 0,1 = 106,65 V.
6. La batterie de stockage se compose de 40 cellules avec une résistance interne rvn = 0,005 Ohm et e. etc. p 2,1 V. La batterie est chargée avec le courant I = 5 A du générateur, par ex. etc. avecsoit 120 V et la résistance interne rg = 0,12 Ohm. Déterminez la résistance supplémentaire rd, la puissance du générateur, la puissance utile de la charge, la perte de puissance dans la résistance supplémentaire rd et la perte de puissance dans la batterie (Fig. 6).
Riz. 6. Calcul de l'accumulateur
Trouver une résistance supplémentaire en utilisant Deuxième loi de Kirchhoff:
Eg = Eb + rd ∙ I + rg ∙ I + 40 ∙ rv ∙ I ; rd = (Eg-Eb-I ∙ (rg + 40 ∙ rv)) / I = (120-84-5 ∙ (0,12 + 0,2)) / 5 = 34,4 / 5 = 6,88 Ohm …
Depuis e. etc. C. Lorsque la batterie est chargée, l'EMF de la cellule au début de la charge est de 1,83 V, puis au début de la charge, avec une résistance supplémentaire constante, le courant sera supérieur à 5 A. Afin de maintenir une charge constante courant, il faut changer la résistance supplémentaire.
Perte de puissance dans la résistance supplémentaire ∆Pd = rd ∙ I ^ 2 = 6,88 ∙ 5 ^ 2 = 6,88 ∙ 25 = 172 W.
Perte de puissance dans le générateur ∆Pg = rg ∙ I ^ 2 = 0,12 ∙ 25 = 3 W.
Perte de puissance dans la résistance interne de la batterie ∆Pb = 40 ∙ rvn ∙ I ^ 2 = 40 ∙ 0,005 ∙ 25 = 5 W.
La puissance fournie du générateur au circuit externe est Pg = Eb ∙ I + Pd + Pb = 84 ∙ 5 + 172 + 5 = 579 W.
Puissance de charge utile Ps = Eb ∙ I = 420 W.