Coefficient de température de résistance

La résistance électrique d'un conducteur dépend généralement du matériau du conducteur, de sa longueur et de sa section, ou, plus brièvement, de la résistance et des dimensions géométriques du conducteur. Cette dépendance est bien connue et s'exprime par la formule :

Connu de tous et Loi d'Ohm pour une section homogène d'un circuit électrique, d'où l'on peut voir que plus la résistance est élevée, plus le courant est faible. Ainsi, si la résistance du fil est constante, alors à mesure que la tension appliquée augmente, le courant doit augmenter de manière linéaire. Mais en réalité ce n'est pas le cas. La résistance des fils n'est pas constante.

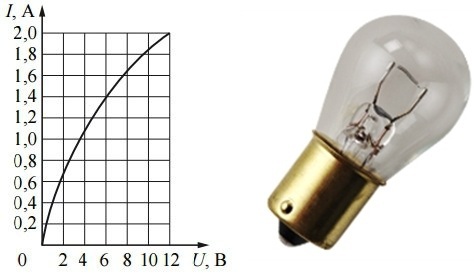
Vous n'avez pas besoin d'aller loin pour trouver des exemples. Si vous connectez une ampoule à une alimentation réglable (avec un voltmètre et un ampèremètre) et augmentez progressivement la tension dessus, en la ramenant à la valeur nominale, vous verrez facilement que le courant ne croît pas linéairement : la tension se rapproche de la valeur nominale de la lampe, le courant à travers sa bobine croît de plus en plus lentement et la lumière devient de plus en plus brillante.

Il n'y a rien de tel que doubler la tension appliquée à la bobine doublera le courant. La loi d'Ohm ne semble pas tenir. En fait, la loi d'Ohm est respectée et exactement la résistance du filament de la lampe n'est pas constante, elle dépend de la température.

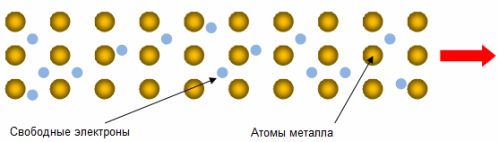
Rappelons quelle est la raison de la conductivité électrique élevée des métaux. Elle est associée à la présence dans les métaux d'un grand nombre de porteurs de charge — composants de courant — électrons de conduction… Ce sont des électrons formés par les électrons de valence des atomes métalliques, qui sont communs à l'ensemble du conducteur, ils n'appartiennent pas à chaque atome individuel.

Sous l'action d'un champ électrique appliqué au conducteur, les électrons de conduction libre passent d'un mouvement chaotique à un mouvement plus ou moins ordonné — un courant électrique se forme. Mais les électrons rencontrent des obstacles sur leur chemin, des inhomogénéités du réseau ionique, comme des défauts de réseau, une structure inhomogène causée par ses vibrations thermiques.

Les électrons interagissent avec les ions, perdent leur élan, leur énergie est transférée aux ions du réseau, transformée en vibrations des ions du réseau, et le chaos du mouvement thermique des électrons eux-mêmes augmente, à partir duquel le conducteur se réchauffe lorsque le courant le traverse.

Dans les diélectriques, les semi-conducteurs, les électrolytes, les gaz, les liquides non polaires, la raison de la résistance peut être différente, mais la loi d'Ohm ne reste évidemment pas linéaire en permanence.

Ainsi, pour les métaux, une augmentation de la température entraîne une augmentation encore plus importante des vibrations thermiques du réseau cristallin, et la résistance au mouvement des électrons de conduction augmente.Cela ressort de l'expérience avec la lampe : la luminosité de la lueur augmente, mais le courant augmente moins. Cela signifie que le changement de température a affecté la résistance du filament de la lampe.

En conséquence, il devient clair que la résistance fils métalliques dépend presque linéairement de la température. Et si l'on tient compte du fait que lorsqu'il est chauffé, les dimensions géométriques du fil changent légèrement, alors la résistance électrique dépend également presque linéairement de la température. Ces dépendances peuvent être exprimées par les formules :

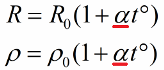
Faisons attention aux probabilités. Supposons qu'à 0°C la résistance du conducteur soit R0, alors à une température t°C il prendra la valeur R(t), et la variation relative de résistance sera égale à α * t°C. Ce facteur de proportionnalité α est appelé coefficient de température de résistance... Il caractérise la dépendance de la résistance électrique de la substance à sa température actuelle.

Ce coefficient est numériquement égal à la variation relative de la résistance électrique d'un conducteur lorsque sa température change de 1K (un degré Kelvin, ce qui équivaut à une variation de température d'un degré Celsius).

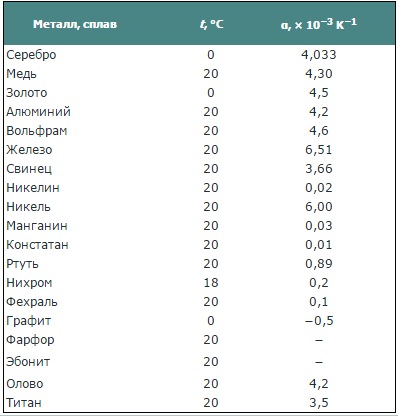
Pour les métaux, le TCR (coefficient de température de la résistance α), bien que relativement faible, est toujours supérieur à zéro, car lorsque le courant passe, les électrons entrent plus souvent en collision avec les ions du réseau cristallin, plus la température est élevée, t .is plus leur mouvement chaotique thermique est élevé et plus leur vitesse est élevée.En entrant en collision dans un mouvement chaotique avec les ions du réseau, les électrons du métal perdent de l'énergie, ce que nous voyons en conséquence - la résistance augmente à mesure que le fil se réchauffe. Ce phénomène est utilisé techniquement dans thermomètres à résistance.

Ainsi, le coefficient de température de résistance α caractérise la dépendance de la résistance électrique de la substance à la température et est mesuré en 1 / K - kelvin à la puissance -1. La valeur de signe opposé est appelée coefficient de température de conductivité.

Quant aux semi-conducteurs purs, le TCS est négatif pour eux, c'est-à-dire que la résistance diminue avec l'augmentation de la température, cela est dû au fait qu'à mesure que la température augmente, de plus en plus d'électrons passent dans la zone de conduction, tandis que la concentration de trous augmente également . Le même mécanisme est caractéristique des diélectriques liquides non polaires et solides.

Les liquides polaires diminuent fortement leur résistance avec l'augmentation de la température en raison d'une diminution de la viscosité et d'une augmentation de la dissociation. Cette propriété est utilisée pour protéger les tubes électroniques des effets destructeurs des courants d'appel élevés.

Pour les alliages, les semi-conducteurs dopés, les gaz et les électrolytes, la dépendance thermique de la résistance est plus complexe que pour les métaux purs. Les alliages à très faible TCS, tels que le manganin et le constantan, sont utilisés dans instruments de mesure électriques.