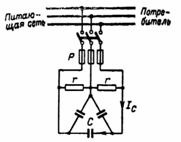
Calculs pour améliorer le facteur de puissance dans un réseau triphasé

Lors du calcul de la capacité d'un condensateur pour améliorer le facteur de puissance dans un réseau triphasé, nous respecterons la même séquence que dans l'article avec des exemples de calculs en réseau monophasé… La valeur du facteur de puissance est déterminée par la formule de puissance pour courant triphasé :

P1 = √3 ∙ U ∙ I ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ I).

Exemples de

1. Un moteur à induction triphasé a les données de panneau suivantes : P = 40 kW, U = 380 V, I = 105 A, η = 0,85, f = 50 Hz. Connexion en étoile du stator. Supposons qu'il soit difficile de déterminer la valeur cosφ de la carte, et qu'il soit donc nécessaire de la déterminer. À quelle valeur le courant diminuera-t-il après avoir amélioré le facteur de puissance à cosφ = 1 à l'aide de condensateurs ? Quelle capacité les condensateurs doivent-ils avoir ? Quelle puissance réactive les condensateurs (Fig. 1) compenseront-ils ?

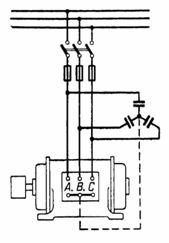
Les pinces de l'enroulement du stator sont marquées: début - C1, C2, C3, extrémités - C4, C5, C6, respectivement.Dans la suite, cependant, pour faciliter la communication avec les schémas, l'origine sera notée A, B, C, et les extrémités X, Y, Z.

Riz. 1.

Puissance moteur P1 = P2 / η = 40000 / 0,85 ≈47000 W,

où P2 est la puissance nette indiquée sur la plaque signalétique du moteur.

cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0,69.

Après avoir amélioré le facteur de puissance à cosφ = 1, la puissance d'entrée sera :

P1 = √3 ∙ U ∙ je ∙ 1

et le courant chutera à

I1 = P1 / (√3 ∙ U) = 47000 / (1,73 ∙ 380) = 71,5 A.

C'est le courant actif à cosφ = 0,69 puisque

Ia = I ∙ cosφ = 105 ∙ 0,69 = 71,5 A.

En figue. 1 montre l'inclusion de condensateurs pour améliorer le cosφ.

Tension du condensateur Uph = U / √3 = 380 / √3 = 220 V.

Le courant magnétisant de phase est égal au courant magnétisant linéaire : IL = I ∙ sinφ = 105 ∙ 0,75 = 79,8 A.

La résistance capacitive du condensateur, qui doit fournir le courant magnétisant, sera : xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).

Par conséquent, la capacité du condensateur C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79,8 / (220 ∙ 3,14 ∙ 100) = 79,800 / (22 ∙ 3,14) ∙ 10 ^ (- 6) = 1156,4 μF.

Un bloc de condensateurs d'une capacité totale de C = 3 ∙ 1156,4≈3469 μF doit être connecté à un moteur triphasé pour améliorer le facteur de puissance à cosφ = 1 et en même temps réduire le courant de 105 à 71,5 A.

La puissance réactive totale compensée par les condensateurs, qui en l'absence de condensateurs est prélevée sur le réseau, Q = 3 ∙ Uph ∙ IL = 3 ∙ 220 ∙ 79,8≈52668 = 52,66 kvar.

Dans ce cas, le moteur consomme de la puissance active P1 = 47 kW uniquement du réseau.

En figue.La figure 2 montre un bloc de condensateurs connectés en triangle et connectés aux bornes d'un moteur triphasé dont l'enroulement est également connecté en triangle. Cette connexion de condensateurs est plus avantageuse que la connexion illustrée à la fig. 1 (voir la conclusion du calcul 2).

Riz. 2.

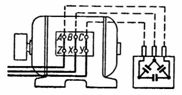
2. Une petite centrale électrique alimente un réseau triphasé avec un courant I = 250 A à une tension réseau U = 380 V et un facteur de puissance réseau cosφ = 0,8. L'amélioration du facteur de puissance est obtenue par des condensateurs qui sont connectés en triangle selon le schéma de la fig. 3. Il est nécessaire de déterminer la valeur de la capacité des condensateurs et la puissance réactive compensée.

Riz. 3.

Puissance apparente S = √3 ∙ U ∙ I = 1,73 ∙ 380 ∙ 250 = 164,3 kVA.

Déterminez la puissance active à cosφ = 0,8 :

P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164,3 ∙ 0,8 = 131,5 W.

Puissance réactive à compenser à cosφ = 0,8

Q = S ∙ sinφ≈164,3 ∙ 0,6 = 98,6 kvar.

Par conséquent, le courant magnétisant linéaire (Fig. 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.

Courant de phase magnétisant (capacitif) ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86,5 A.

Le courant du condensateur peut être déterminé d'une autre manière par le courant magnétisant (réactif) dans le circuit :

IL = je ∙ sinφ = 250 ∙ 0,6 = 150 A,

ICph = ILph = IL / √3 = 150 / 1,73 = 86,7 A.

Lorsqu'il est connecté en triangle, chaque groupe de condensateurs a une tension de 380 V et un courant de phase ICph = 86,7 A.

Je = ICf = U / xC = U / (1⁄ (ω ∙ C)) = U ∙ ω ∙ C.

Par conséquent, C = IC / (U ∙ 2 ∙ π ∙ f) = 86,7 / (300 ∙ π ∙ 100) = 726 μF.

La capacité totale de la batterie de condensateurs est C3 = 3 ∙ 726 = 2178 μF.

Les condensateurs connectés permettent d'utiliser toute la puissance de la centrale S = 164,3 kVA sous forme de puissance nette.Sans condensateurs de fonctionnement, seule une puissance active de 131,5 kW est utilisée à cosφ = 0,8.

La puissance réactive compensée Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 augmente proportionnellement au carré de la tension. Par conséquent, la capacité requise des condensateurs, et donc le coût des condensateurs, est plus faible car la tension est plus élevée.

Les résistances r de la fig. 3 permettent de décharger progressivement les condensateurs lorsqu'ils sont déconnectés du réseau.