Calcul de la capacité du condensateur
 La capacité C est la capacité du condensateur à accepter (stocker et retenir) la quantité d'électricité Q en ampères-secondes ou la charge Q en pendentifs. Si vous indiquez à un corps, par exemple une balle, une charge électrique (quantité d'électricité) Q, alors un électroscope connecté entre ce corps et la terre indiquera une tension U (Fig. 1). Cette tension est proportionnelle à la charge et dépend également de la forme et de la taille du corps.
La capacité C est la capacité du condensateur à accepter (stocker et retenir) la quantité d'électricité Q en ampères-secondes ou la charge Q en pendentifs. Si vous indiquez à un corps, par exemple une balle, une charge électrique (quantité d'électricité) Q, alors un électroscope connecté entre ce corps et la terre indiquera une tension U (Fig. 1). Cette tension est proportionnelle à la charge et dépend également de la forme et de la taille du corps.
La relation entre la charge Q et la tension U est exprimée par la formule Q = C ∙ U.
La constante de proportionnalité C s'appelle la capacité du corps. Si le corps a la forme d'une boule, la capacité du corps est proportionnelle au rayon de la boule r.
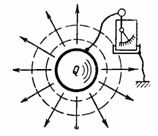
Riz. 1.
L'unité de mesure de la capacité est le farad (F).
Le corps a une capacité de 1 F lorsqu'une charge de 1 k produit une tension de 1 V entre lui et la masse. Les farads sont une très grande unité de mesure, donc des unités plus petites sont utilisées dans la pratique : microfarad (μF), nanofarad (nF) et picofarad (pF)...
Ces unités sont liées par les rapports suivants : 1 Ф = 10 ^ 6 μF ; 1 μF = 10 ^ 6 pF ; 1 nF = 10 ^ 3 pF.
La capacité d'une boule de 1 cm de rayon est de 1,1 pF.
Non seulement un corps isolé peut accumuler une charge, mais également un dispositif spécial appelé condensateur. Un condensateur se compose de deux plaques ou plus (plaques) séparées par un diélectrique (isolation).
En figue. 2 montre un circuit avec une source continue connectée à un condensateur. Lorsqu'il est allumé, une charge positive +Q est formée dans la plaque de droite du condensateur et une charge négative -Q dans la plaque de gauche. Pendant charge du condensateur un courant circule dans le circuit, qui s'arrête après la fin de la charge ; alors la tension aux bornes du condensateur sera égale à e. etc. c) source U. La charge sur la plaque du condensateur, la tension et la capacité sont liées par le rapport Q = C ∙ U. Dans ce cas, un champ électrostatique se forme dans le diélectrique du condensateur.
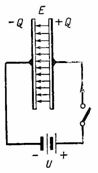
Riz. 2.
La capacité d'un condensateur avec un diélectrique à air peut être calculée par la formule C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, où S est l'aire d'une plaque, cm2; d est la distance entre les plaques, cm; C est la capacité du condensateur, pF.
La capacité d'un condensateur constitué de n plaques (Fig. 3) est égale à : C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.
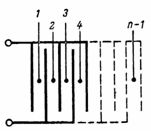
Riz. 3.
Si l'espace entre les plaques est rempli d'un autre diélectrique, par exemple du papier, la capacité du condensateur augmentera d'un facteur ε. Lorsque l'isolation en papier est utilisée, la capacité augmentera de 3 fois, avec une isolation en mica - 5 à 8 fois, avec du verre - 7 fois, etc. La valeur de ε est appelée la constante diélectrique du diélectrique.
La formule générale pour déterminer la capacité d'un condensateur à constante diélectrique ε (epsilon) est : C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.
Cette formule est utile pour calculer les petits condensateurs variables pour les radios.La même formule peut être représentée par : C = (ε_0 ∙ ε ∙ S) / d, où ε_0 est la constante diélectrique ou la constante diélectrique du vide (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m) ; ε est la constante diélectrique du diélectrique.
Dans cette formule, les dimensions sont remplacées en mètres et la capacité est obtenue en farads.
Exemples de
1. Quelle est la capacité de la planète Terre, dont le rayon est r = 6378 km ?
Puisque la capacité d'une sphère de rayon 1 cm est égale à 1,11 pF, la capacité de la Terre est : C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (La capacité d'une boule de la taille de notre planète est relativement petite. Les condensateurs électrolytiques de petite taille ont cette capacité).
2. Déterminez la capacité d'un condensateur composé de deux plaques, chacune ayant une surface S = 120 cm2.
Les plaques sont séparées par une couche d'air d'une épaisseur de d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF .. .
3. Déterminez la capacité du condensateur avec les données données dans l'exemple précédent, si l'espace entre les plaques est rempli de papier ciré avec une constante diélectrique ε = 4, verre (ε = 7), carton électrique (ε = 2) , mica (ε = 8 ).
Un condensateur en papier ciré a une capacité C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.
La capacité d'un condensateur en verre est C = 7 ∙ 21,2 = 148,4 pF.
La capacité du condensateur en carton est C = 2 ∙ 21,2 = 42,3 pF.
La capacité du condensateur mica est C = 8 ∙ 21,2 = 169,6 pF.
4. Quelle est la capacité d'un condensateur rotatif à air pour un récepteur radio composé de 20 plaques d'une surface de 20 cm2 si la distance entre les plaques est de 0,06 cm (Fig. 149)?
C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.
Le condensateur représenté sur la Fig.3, se compose de condensateurs séparés les plus simples à deux plaques, dont le nombre est égal à n-1.
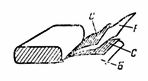
5. Un condensateur en papier de capacité C = 2 μF se compose de deux bandes de papier d'aluminium C et de deux bandes d'un diélectrique en papier ciré B avec une constante diélectrique ε = 6. L'épaisseur du papier ciré est d = 0,1 mm. Les bandes pliées sont enroulées, les fils sont fabriqués à partir des plaques d'acier. Déterminez la longueur de la bande d'acier du condenseur si sa largeur est de 4 cm (Fig. 4).
Riz. 4.
Tout d'abord, nous déterminons l'aire d'une bande par la formule C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, d'où S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11) ; S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37 680 cm2.
La longueur de chaque bande est l = 37680/4 = 9420 cm = 94,2 m.