Calcul du potentiomètre et du shunt composé

Concepts et formules

Un potentiomètre est une résistance variable avec un curseur qui est inclus comme indiqué sur la fig.

Pour plus de détails voir — Potentiomètres et leurs applications

Une tension U est appliquée aux points 1 et 2. Une tension réglable est prélevée aux points 2 et 3 dont la valeur est inférieure à U et dépend de la position du curseur. Les diviseurs de tension ont un schéma similaire, mais ils ne sont pas réglables et n'ont pas de curseur mobile.

Les potentiomètres, les diviseurs de tension et les shunts complexes sont calculés à l'aide de Les lois de Kirchhoff, comme le calcul des circuits classiques avec des résistances.

Exemples de

1. La tension source est U = 24 V, la résistance totale du potentiomètre est r = 300 Ohm. Le moteur est monté séparément de sorte que r1 = 50 ohms. Quelle tension U1 peut être retirée des points 3 et 2 (Fig. 1) ?

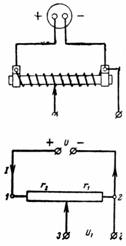
Riz. 1.

Le courant I et la tension U aux bornes de la résistance r sont liés par la formule I ∙ r = U.

Le curseur du potentiomètre sépare une partie de la résistance, c'est-à-dire. la résistance r1. La chute de tension entre les points 3 et 2 est égale à I ∙ r1 = U1.

A partir du rapport de la chute de tension, on obtient l'égalité (I ∙ r1) / (I ∙ r) = U1 / U. Plus la résistance r1 est grande, plus la valeur de la tension U1 entre les points 3 et 2 est grande U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. Le potentiomètre (Fig. 2) est chargé sur une lampe avec une résistance r = 100 Ohm. Le potentiomètre est divisé par un curseur en deux parties avec r1 = 600 Ohm et r2 = 200 Ohm. Déterminer la tension Ul et le courant de la lampe Il.

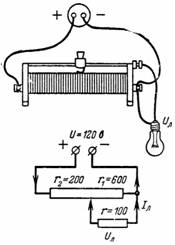
Riz. 2.

Le courant I traverse la résistance r2 et le courant Il traverse la lampe. Un courant I-Il traverse la résistance r1, ce qui crée une tension aux bornes de la résistance r1 égale à la tension de la lampe : (I-Il) ∙ r1 = Ul.

D'autre part, la tension de la lampe est égale à la tension de la source moins chute de tension à la résistance r2 : U-I ∙ r2 = Ul.

Le courant I est égal à la tension de la source divisée par la résistance résultante de la connexion série-parallèle des résistances :

je = U / (r2 + (r ∙ r1) / (r + r1)).

Nous substituons l'expression du courant total de la source dans la deuxième équation :

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Après la transformation, nous obtenons une expression pour la tension de la lampe :

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Si nous transformons cette expression, partant du fait que Ul = Il ∙ r, alors nous obtenons une expression pour le courant de lampe :

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Remplacez les valeurs numériques dans les équations résultantes :

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V ;

Il = Ul / r = 36/100 = 0,36 A.

3. Calculez la tension Up et le courant Ip de l'appareil de mesure qui est connecté à une partie du potentiomètre. L'appareil a une résistance de r = 1000 Ohm. Le point de branchement divise la résistance du diviseur en r2 = 500 ohms et r1 = 7000 ohms (Fig. 3).Tension aux bornes du potentiomètre U = 220 V.

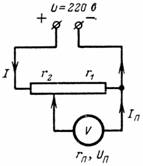
Riz. 3.

En utilisant les formules obtenues précédemment, on peut écrire que le courant traversant l'appareil est :

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000)= 1540000/11000000 = 1,54 / 11 = 0,14 A.

Up = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Calculez la tension de l'appareil Up, s'il consomme un courant Ip = 20 mA et est relié à un potentiomètre divisé en résistances r2 = 10 ^ 4 Ohm et r1 = 2 ∙ 10 ^ 4 Ohm (Fig. 3).

La tension totale dans le diviseur de tension est égale à la somme des chutes de tension dans ses parties (à travers les résistances r1 et r2) : U = I ∙ r2 + I1 ∙ r1 ; U = je ∙ r2 + haut

Le courant source est dérivé au point de contact moteur : I = I1 + Ip ; I = Upn / r1 + In.

Nous substituons la valeur du courant I dans l'équation de tension :

U = (Un / r1 + In) ∙ r2 + Un ;

U = Uï / r1 ∙ r2 + Iï ∙ r2 + Uï ;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Par conséquent, la tension de l'appareil Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Remplacez les valeurs numériques : Up = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. Une source de courant continu avec une tension U = 120 V alimente les circuits d'anode du récepteur radio via un potentiomètre (diviseur de tension) qui, avec le filtre, a une résistance de r = 10000 Ohm. La tension U1 est supprimée par la résistance r2 = 8000 Ohm. Calculer la tension d'anode à vide et au courant de charge I = 0,02 A (Fig. 4).

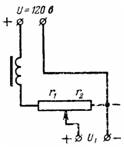
Riz. 4.

Le premier cas est similaire à l'exemple 1 :

U : U1 = r : r2 ;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Le second cas est similaire à l'exemple 3 :

U1 = (U-I ∙ r1) / r ∙ r2 ;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Lors de la charge, la tension chutera de 96 à 64 V.Si plus de tension est nécessaire, le curseur doit être déplacé vers la gauche, c'est-à-dire que la résistance r2 doit être augmentée.

6. Les tensions Ua et Ub sont supprimées par le diviseur de tension. La résistance totale du diviseur de tension connecté à la tension U1 = 220 V est r = 20 000 Ohm. Quelle est la tension Ua dans la résistance r3 = 12000 Ohm avec une consommation de courant Ia = 0,01 A et la tension Ub dans la résistance r2 + r3 = 18000 Ohm avec une consommation de courant Ib = 0,02 A (Fig. 5).

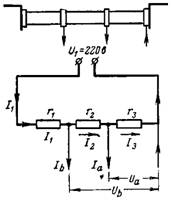
Riz. 5.

Résistance de tension r3

Ua = I3 ∙ r3 ;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3 ;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

La tension Ub est égale à la somme de la chute de tension Ua aux bornes de la résistance r3 et de la chute de tension aux bornes de la résistance r2. La chute de tension aux bornes de la résistance r2 est égale à I2 ∙ r2. Courant I2 = Ia + I3. Le courant I3 peut être calculé comme dans l'exemple 1 :

I3 = (220-80-40) / 20 000 = 0,005 A ;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Tension Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

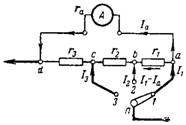
7. Calculez le shunt combiné pour le milliampèremètre de sorte qu'à différentes positions de l'interrupteur, il ait les plages de mesure suivantes : I1 = 10 mA ; I2 = 30mA ; I3 = 100mA. Le schéma de connexion du shunt est illustré à la fig. 6. Résistance interne de l'appareil ra = 40 Ohm. Plage de mesure intrinsèque du milliampèremètre 2 mA.

Riz. 6.

Lors de la mesure du courant I≤2mA, le shunt est désactivé.

a) Lors de la mesure du courant I = 10 mA, l'interrupteur est en position 1 et un courant de 10-2 = 8 mA traverse toutes les résistances shunt. La chute de tension aux bornes de la résistance shunt Ush et du dispositif Ua entre les points d et a doit être la même

Ush = Ua ;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra ;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Lors de la mesure du courant I2 = 30 mA, le commutateur est en position 2. Le courant mesuré se divisera au point b. A pleine déflexion de l'aiguille de l'appareil, le courant Ia = 2 mA traversera la résistance r1 et l'appareil ra.

Le reste du courant I2-Ia passera par les résistances r2 et r3. Les courants vont créer la même chute de tension sur les deux branches entre les points d et b :

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra ;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) De la même manière, nous effectuerons le calcul en augmentant la plage de mesure à I3 = 100 mA. Le courant I3-Ia traversera la résistance r3 et le courant Ia traversera les résistances r1, r2, ra. La tension dans les deux branches est la même : (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra ;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Nous avons obtenu trois équations avec trois valeurs inconnues des résistances r1, r2 et r3.

Nous multiplions toutes les équations par 1000 et les convertissons :

r1 + r2 + r3 = 10 ;

14 ∙ (r2 + r3) -r1 = 40 ;

49 ∙ r3-r1-r2 = 40.

Ajoutons les première et troisième équations : 50 ∙ r3 = 50 ;

r3 = 50/50 = 1 ohm.

Ajoutons les première et seconde équations : 15 ∙ r2 + 15 ∙ r3 = 50 ;

15 ∙ r2 + 15 ∙ 1 = 50 ;

15 ∙ r2 = 35 ; r2 = 2,34 ohms.

Substituons les résultats obtenus dans la première équation : r1 + 35/15 + 1 = 10 ;

15 ∙ r1 + 35 + 15 = 150 ;

r1 = 100/15 = 6,66 ohms.

L'exactitude du calcul peut être vérifiée en remplaçant les valeurs de résistance obtenues dans les équations.