Rigidité diélectrique de l'isolant. Exemples de calcul

Avec une augmentation progressive de la tension U entre des conducteurs séparés par un diélectrique (isolant), par exemple des plaques de condensateur ou des fils de câbles conducteurs, l'intensité (force) du champ électrique dans le diélectrique augmente. L'intensité du champ électrique dans le diélectrique augmente également à mesure que la distance entre les fils diminue.

À une certaine intensité de champ, une panne se produit dans le diélectrique, une étincelle ou un arc se forme et un courant électrique apparaît dans le circuit. L'intensité du champ électrique à laquelle se produit le claquage de l'isolant est appelée rigidité diélectrique Epr de l'isolant.

La rigidité diélectrique est définie comme la tension par mm d'épaisseur d'isolant et est mesurée en V/mm (kV/mm) ou kV/cm. Par exemple, la rigidité diélectrique de l'air entre plaques lisses est de 32 kV/cm.

L'intensité du champ électrique dans un diélectrique pour le cas où les conducteurs se présentent sous la forme de plaques ou de bandes séparées par un espace égal (par exemple, dans un condensateur en papier) est calculée par la formule

E = U / d,

où U est la tension entre les fils, V (kV); d — épaisseur de la couche diélectrique, mm (cm).

Exemples de

1. Quelle est l'intensité du champ électrique dans l'entrefer de 3 cm d'épaisseur entre les plaques si la tension entre elles est U = 100 kV (Fig. 1) ?

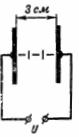
Riz. 1.

L'intensité du champ électrique est : E = U/d = 100000/3 = 33333 V/cm.

Une telle tension dépasse la rigidité diélectrique de l'air (32 kV/cm) et il y a un risque de destruction.

Le risque d'endommagement par courant continu peut être évité en augmentant l'écart à, par exemple, 5 cm, ou en utilisant une autre isolation plus solide au lieu de l'air, comme du carton électrique (Fig. 2).

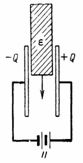
Riz. 2.

Le carton électrique a une constante diélectrique de ε = 2 et une rigidité diélectrique de 80 000 V/cm. Dans notre cas, l'intensité du champ électrique dans l'isolant est de 33333 V. L'air ne peut pas supporter cette force, alors que le carton électrique a dans ce cas une réserve de rigidité diélectrique de 80 000/33333 = 2,4, car la rigidité diélectrique du boîtier électrique est 80 000/32 000 = 2,5 fois celui de l'air.

2. Quelle est l'intensité du champ électrique dans le diélectrique d'un condensateur de 3 mm d'épaisseur si le condensateur est connecté à une tension U = 6 kV ?

E = U/d = 6000/0,3 = 20000 V/cm.

3. Un diélectrique d'une épaisseur de 2 mm casse à une tension de 30 kV. Quelle était sa puissance électrique ?

E = U/d = 30 000/0,2 = 150 000 V/cm = 150 kV/cm. Le verre a une telle force électrique.

4. L'espace entre les plaques du condensateur est rempli de couches de carton électrique et d'une couche de mica de même épaisseur (Fig. 3). La tension entre les plaques du condensateur est U = 10000 V. Le carton électrique a une constante diélectrique ε1 = 2 et le mica ε2 = 8.Comment la tension U sera-t-elle répartie entre les couches d'isolation et quelle intensité aura le champ électrique dans les couches individuelles ?

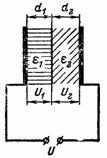
Riz. 3.

Les tensions U1 et U2 aux bornes de couches diélectriques de même épaisseur ne seront pas égales. La tension du condensateur sera divisée en tensions U1 et U2, qui seront inversement proportionnelles aux constantes diélectriques :

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4 ;

U1 = 4 ∙ U2.

Puisque U = U1 + U2, nous avons deux équations à deux inconnues.

Remplacez la première équation par la seconde : U = 4 ∙ U2 + U2 = 5 ∙ U2.

Donc, 10000 V = 5 ∙ U2 ; U2 = 2000 V ; U1 = 4, U2 = 8000V.

Bien que les couches diélectriques aient la même épaisseur, elles ne sont pas également chargées. Un diélectrique avec une constante diélectrique plus élevée est moins chargé (U2 = 2000 V) et inversement (U1 = 8000 V).

L'intensité du champ électrique E dans les couches diélectriques est égale à :

E1 = U1 / d1 = 8 000 / 0,2 = 40 000 V/cm ;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V/cm.

La différence de constante diélectrique entraîne une augmentation de l'intensité du champ électrique. Si tout l'espace était rempli d'un seul diélectrique, par exemple du mica ou du carton électrique, l'intensité du champ électrique serait plus faible, car il serait réparti assez uniformément dans l'espace :

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V/cm.

Il faut donc éviter l'utilisation d'isolants complexes avec des constantes diélectriques très différentes. Pour la même raison, le risque de défaillance augmente lorsque des bulles d'air se forment dans l'isolant.

5. Déterminez l'intensité du champ électrique dans le diélectrique du condensateur à partir de l'exemple précédent si l'épaisseur des couches diélectriques n'est pas la même.Le tableau électrique a une épaisseur d1 = 0,2 mm et mica d2 = 3,8 mm (Fig. 4).

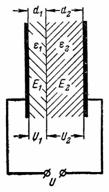
Riz. 4.

L'intensité du champ électrique sera distribuée inversement proportionnelle aux constantes diélectriques :

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Puisque E1 = U1 / d1 = U1 / 0,2 et E2 = U2 / d2 = U2 / 3,8, alors E1 / E2 = (U1 / 0,2) / (U2 / 3,8) = (U1 ∙ 3,8) / (0,2 ∙ U2) = 19 ∙ U1 / U2.

Donc E1 / E2 = 4 = 19 ∙ U1 / U2, soit U1 / U2 = 4/19.

La somme des tensions U1 et U2 sur les couches diélectriques est égale à la tension de source U : U = U1 + U2 ; 10000 = U1 + U2.

Puisque U1 = 4/19 ∙ U2, alors 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2 ; U2 = 190 000 /23 = 8260 V ; U1 = U-U2 = 1740V.

L'intensité du champ électrique dans le mica est E2 ∙ 8260 / 3,8≈2174 V / cm.

Le mica a une rigidité diélectrique de 80 000 V/mm et peut supporter une telle tension.

L'intensité du champ électrique dans le carton électrique est E1 = 1740 / 0,2 = 8700 V / mm.

Le carton électrique ne résistera pas à une telle tension, puisque sa rigidité diélectrique n'est que de 8000 V/mm.

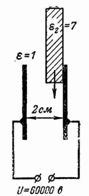
6. Une tension de 60 000 V est connectée à deux plaques métalliques distantes de 2 cm Déterminer l'intensité du champ électrique dans l'entrefer, ainsi que l'intensité du champ électrique dans l'air et le verre s'il y a du verre dans l'espace insère une plaque avec une épaisseur de 1 cm (Fig. 5).

Riz. 5.

S'il n'y a que de l'air entre les plaques, l'intensité du champ électrique dans celui-ci est égale à : E = U / d = 60 000 /2 = 30 000 V / cm.

L'intensité du champ est proche de la rigidité diélectrique de l'air.Si une plaque de verre de 1 cm d'épaisseur (constante diélectrique du verre ε2 = 7) est introduite dans l'entrefer, alors E1 = U1 / d1 = U1 / 1 = U1 ; E2 = U2 / d2 = U2 / 1 = U2 ; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2 ;

U1 = 7 ∙ U2 ; U1 = 60 000-U2 ; 8 ∙ U2 = 60 000 ; U2 = 7500 V ; E2 = U2/d2 = 7500 V/cm.

L'intensité du champ électrique dans le verre est E2 = 7,5 kV/cm, et sa rigidité diélectrique est de 150 kV/cm.

Dans ce cas, le verre a un facteur de sécurité de 20 fois.

Pour l'entrefer nous avons : U1 = 60 000-7 500 = 52 500 V ; E1 = U1/d1 = 52500 V/cm.

Dans ce cas, l'intensité du champ électrique dans l'entrefer est plus importante que dans le premier, sans verre. Une fois le verre inséré, l'ensemble de la combinaison a moins de résistance que l'air seul.

Le risque de casse survient également lorsque l'épaisseur de la plaque de verre est égale à l'écart entre les plaques conductrices, c'est-à-dire 2 cm, car il y aura inévitablement de minces lames d'air dans l'interstice qui sera crevé.

La rigidité diélectrique de l'interstice entre les conducteurs haute tension doit être renforcée avec des matériaux à faible constante diélectrique et à forte rigidité diélectrique, par exemple du carton électrique avec ε = 2. Eviter les combinaisons de matériaux à forte constante diélectrique (verre , porcelaine) et de l'air, qui doit être remplacé par de l'huile.