Calculs de circuits magnétiques

Dans les machines et appareils électriques, le flux magnétique F est concentré dans le circuit magnétique (noyau ferromagnétique) et les entrefers de ce circuit magnétique. Ce chemin de flux magnétique s'appelle un circuit magnétique.

Un circuit magnétique est comme un circuit électrique. Le flux magnétique Ф ressemble à un courant électrique I, l'induction В ressemble à une densité de courant, la force magnétisante (ns) Fн (H ∙ l = I ∙ ω) correspond à e. etc. avec

Dans le cas le plus simple, le circuit magnétique a partout la même section et est constitué d'un matériau magnétique homogène. Pour déterminer n. avec l ∙ ω nécessaire pour fournir l'induction requise B, l'intensité correspondante H est déterminée à partir de la courbe d'aimantation et multipliée par la longueur moyenne de la ligne de champ magnétique l : H ∙ l = I ∙ ω = Fm.

À partir de là, le courant requis I ou le nombre de tours ω de la bobine est déterminé.

Un circuit magnétique complexe comporte généralement des sections avec des sections et des matériaux magnétiques différents. Ces sections sont généralement connectées en série, donc le même flux magnétique F traverse chacune d'elles.L'induction B dans chaque section dépend de la section transversale de la section et est calculée pour chaque section séparément par la formule B = Φ∶S.

Pour différentes valeurs d'induction, l'intensité H est déterminée à partir de la courbe d'aimantation et multipliée par la longueur moyenne de la ligne électrique de la section correspondante du circuit. En résumant les œuvres individuelles, on obtient le n complet. c. circuit magnétique :

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … qui détermine le courant magnétisant ou le nombre de tours de bobine.

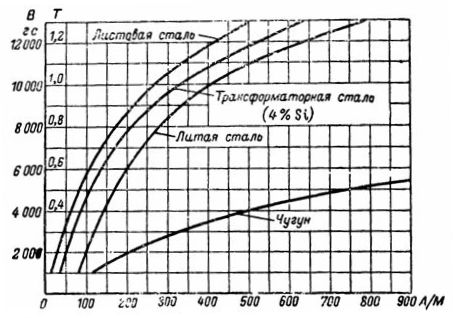
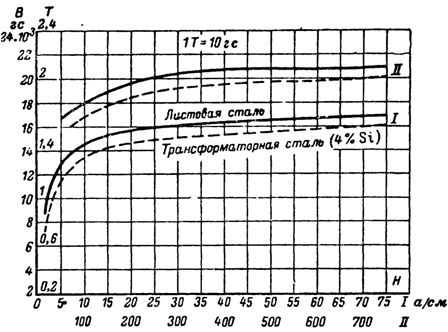
Courbes d'aimantation

Exemples de

1. Quel doit être le courant magnétisant I d'une bobine de 200 tours pour que n. c) créer dans l'anneau en fonte un flux magnétique Ф = 15700 Ms = 0,000157 Wb ? Le rayon moyen de l'anneau en fonte est r = 5 cm et le diamètre de sa section est d = 2 cm (Fig. 1).

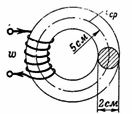
Riz. 1.

Section du circuit magnétique S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

L'induction dans le noyau est : B = Φ∶S = 15700∶3.14 = 5000 G.

Dans le système MKSA, l'induction est de : B = 0,000157 Wb : 0,0000314 m2 = 0,5 T.

A partir de la courbe d'aimantation de la fonte, on trouve l'intensité requise H égale à 750 A/m pour B = 5000 G = 0,5 T. L'intensité magnétisante est égale à : I ∙ ω = H ∙ l = 235,5 Av.

Par conséquent, le courant requis I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Un circuit magnétique fermé (Fig. 2) est constitué de plaques d'acier d'un transformateur. Combien de spires doit-il y avoir dans une bobine avec un courant de 0,5 A pour créer un flux magnétique dans le noyau Ф = 160000 Ms = 0,0016 Wb ?

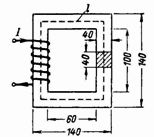
Riz. 2.

Section centrale S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Induction du noyau B = F / S = 160000/16 = 10000 Gs = 1 T.

D'après la courbe d'aimantation de l'acier du transformateur, on trouve pour B = 10 000 Gs = 1 T l'intensité H = 3,25 A/cm = 325 A/m.

La longueur moyenne de la ligne de champ magnétique est l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Force magnétisante Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Av.

A un courant de 0,5 A, le nombre de spires est ω = 156 / 0,5 = 312.

3. Le circuit magnétique illustré à la fig. 3 est similaire au circuit magnétique de l'exemple précédent, sauf qu'il présente un entrefer de δ = 5 mm. Que ne devrait-il pas être. s et le courant de la bobine pour que le flux magnétique soit le même que dans l'exemple précédent, c'est-à-dire F = 160000 Ms = 0,0016 Wb ?

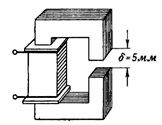
Riz. 3.

Le circuit magnétique comporte deux tronçons connectés en série dont la section est la même que dans l'exemple précédent, soit S = 16 cm2. L'inductance est également égale à B = 10000 G = 1 T.

La longueur moyenne de la ligne magnétique en acier est légèrement plus courte : lс = 48-0,5 = 47,5 cm ≈0,48 m.

La tension magnétique dans cette section du circuit magnétique est Hc ∙ lc = 3,25 ∙ 48≈156 Av.

L'intensité du champ dans l'entrefer est : Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A/cm.

La tension magnétique dans la section transversale de l'entrefer Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Av.

Complète n. c est égal à la somme des tensions magnétiques dans les sections individuelles : I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. je = (je ∙ ω) / ω = 4156/312 = 13,3 A.

Si dans l'exemple précédent le flux magnétique requis était fourni par un courant de 0,5 A, alors pour un circuit magnétique avec un entrefer de 0,5 cm un courant de 13 A est nécessaire pour obtenir le même flux magnétique. On en déduit qu'un entrefer, même insignifiant par rapport à la longueur du circuit magnétique, augmente fortement le n requis. v. et courant de bobine.

4. Le flux magnétique du transformateur est calculé comme étant F = 72000 Ms. Le calcul de n est nécessaire.s.et courant magnétisant de l'enroulement primaire ayant 800 tours. Il y a un espace δ = 0,2 mm dans le noyau du transformateur. Les dimensions du noyau du transformateur sont indiquées à la fig. 4. Section transversale du noyau S = 2 ∙ 3 ​​= 6 cm2 (les transformateurs avec des noyaux de cette forme sont appelés blindés).

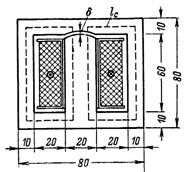
Riz. 4.

Induction noyau et entrefer B = F / S = 72000/6 = 12000 G.

D'après la courbe d'aimantation de l'acier du transformateur pour B = 12000 G, on détermine l'intensité : Hc = 5 A/cm.

La longueur moyenne de la ligne magnétique dans l'acier est lс = 2 ∙ (6 + 3) = 18 cm.

Tension dans l'entrefer Hδ = 0,8 ∙ B = 9600 A/cm.

Force magnétisante I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av ; je = (je ∙ ω) / ω = 282/800 = 0,35 A.

Dans le noyau blindé, le flux magnétique se divise en deux parties, qui sont fermées le long des tiges latérales, dont la section transversale est S / 2, et la longueur moyenne de la ligne magnétique est lc. De ce fait, le circuit magnétique est tout à fait analogue au circuit magnétique d'un transformateur classique avec un noyau commun S et une longueur de ligne électrique lc.

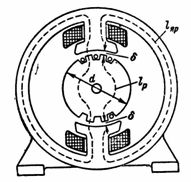
5. Le flux magnétique de la machine à courant continu F = 1280000 Mks. Le circuit magnétique contient une culasse en acier coulé avec une longueur de ligne magnétique moyenne la = 80 cm, un rotor assemblé à partir de plaques d'acier électrique avec une longueur de champ moyenne lр = 18 cm et deux entrefers δ 0,2 cm chacun. = 8 ∙ 20 cm2 ; rotor et section polaire Sð = 12 ∙ 20 cm2... Calculer n. p et le nombre de tours de la bobine polaire, si le courant magnétisant (excitant) maximal dans celle-ci est de 1 A (Fig. 5).

Riz. 5.

Induction dans la culasse et le pôle Bя = Ф / Sя = 1280000/160 = 8000 G.

La tension dans la culasse et le pôle selon la courbe d'aimantation de l'acier moulé à Bя = 8000 G est égale à :

H = 2,8 A/cm.

La force d'aimantation dans la section de la culasse HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Induction dans le rotor, le pôle et l'entrefer Br = Ф / Ср = 1280000/240 = 5333 G.

Tension dans un rotor constitué de plaques d'acier à Br = 5333 Gs Hrp = 0,9 A / cm,

et la tension magnétique de la section du rotor Hр ∙ lр = 0,9 ∙ 18 = 16,2 Av.

Tension dans l'entrefer Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A/cm.

La tension magnétique dans la section transversale de l'entrefer Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Complète n. c) égale à la somme des tensions magnétiques dans des sections distinctes : I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ ; Je ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 Av.

Le nombre de spires dans les bobines bipolaires ω = (I ∙ ω) / I = 1946,76 / 1≈2000.