Processus oscillatoire en électrotechnique et électronique, types d'oscillations
Processus oscillatoire - un processus avec divers degrés de répétabilité. Tous les processus oscillatoires sont divisés en 2 classes : périodiques et non périodiques. En théorie, ils utilisent également une classe intermédiaire - les oscillations presque périodiques.
Un processus oscillatoire est dit périodique, dans lequel la valeur caractérisant ce processus, prise à tout instant, après un certain laps de temps T a la même valeur.
La fonction f (t), qui est une expression mathématique du processus oscillatoire, est dite périodique de période T si elle satisfait la condition f (t + T) = f (t).
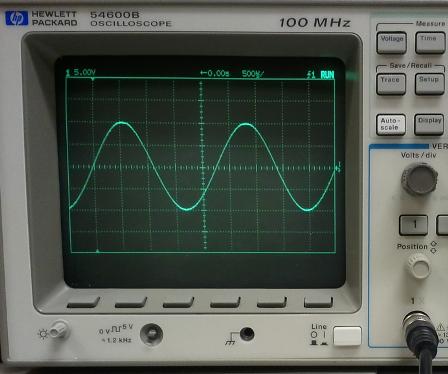
Parmi la classe des processus oscillatoires périodiques, le rôle principal est joué par les oscillations harmoniques ou sinusoïdales, dans lesquelles un changement d'une grandeur physique avec le temps se produit selon la loi du sinus ou du cosinus. Leur bilan global est de :
y = f (t) = aCos ((2π / T) t — φ),
où a — amplitude des oscillations, φ est la phase d'oscillation, 1/T = f — fréquence et 2πf = ω — fréquence des vibrations cycliques ou circulaires.
Application des oscillations sinusoïdales et de leurs caractéristiques :
Paramètres de base du courant alternatif
Manières graphiques d'afficher le courant alternatif
Une fonction quasi périodique correspondant à une lecture d'oscillations périodiques est définie par la condition :
| f · (t + τ) — f (t) | <= ε où ε — attribue une valeur à chaque valeur T.
La quantité τ dans ce cas est appelée presque période. Si la valeur ε est très petite par rapport à la valeur moyenne de f (t) à l'instant T, alors la fonction quasi-périodique sera proche de la périodique.
Les oscillations non périodiques sont beaucoup plus variées que les périodiques. Mais le plus souvent en automatisation on doit rencontrer des oscillations sinusoïdales amortissantes ou croissantes.
Les oscillations selon la loi de la sinusoïde amortie ou, comme on les appelle parfois, les oscillations harmoniques amorties, peuvent être représentées sous une forme générale :
x = Ae-δTcos·(ω + φ),
où t est le temps, A et φ sont des constantes arbitraires. La notation générale de la loi des oscillations harmoniques croissantes ne diffère que par le signe du facteur d'amortissement δ[1 seconde].
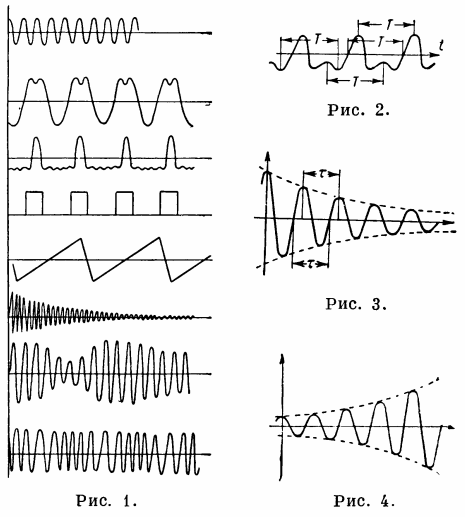
Figue. 1 — processus oscillant, Fig. 2. — processus périodique, fig. 3. — oscillations harmoniques décroissantes, fig. 4. — augmentation des oscillations harmoniques.
Un exemple d'application du processus oscillatoire est le circuit oscillatoire le plus simple.
Circuit oscillateur (circuit électrique) - un circuit électrique passif dans lequel des oscillations électriques peuvent se produire avec une fréquence déterminée par les paramètres du circuit lui-même.
Le circuit oscillant le plus simple est constitué de la capacité C et de l'inductance L. En l'absence d'influence extérieure, amortit les oscillations avec la fréquence εО = 1/2π√LC.
L'amplitude des vibrations diminue avec par exemple -δT, où δ est le coefficient d'amortissement. Si δ> = eO, alors les oscillations amorties dans le circuit deviennent non périodiques.
En électronique, la qualité du circuit oscillant est déterminée par le facteur de qualité : Q = nf/δ... Lorsqu'une force périodique externe agit sur le circuit oscillant, des oscillations forcées se produisent dans celui-ci. L'amplitude des oscillations forcées augmente considérablement pour les circuits à Q élevé si la fréquence de l'influence externe est proche de eo (résonance). Le circuit oscillant est l'une des pièces principales des amplificateurs résonnants, générateurs et autres appareils électroniques.
Voir aussi sur ce sujet : Application de la résonance de tension et de la résonance de courant
