Qu'est-ce que le courant alternatif et en quoi diffère-t-il du courant continu

Courant alternatif, Par contre courant DC, change constamment à la fois en amplitude et en direction, et ces changements se produisent périodiquement, c'est-à-dire qu'ils se répètent à des intervalles exactement égaux.

Pour induire un tel courant dans le circuit, utilisez des sources de courant alternatif qui créent une force électromotrice alternative, changeant périodiquement d'amplitude et de direction.Ces sources sont appelées alternateurs.

En figue. 1 montre un schéma de dispositif (modèle) de la plus simple alternateur. 

Un cadre rectangulaire en fil de cuivre, fixé sur l'axe et mis en rotation sur le terrain à l'aide d'un entraînement par courroie aimant… Les extrémités du cadre sont soudées à des anneaux de cuivre qui, en tournant avec le cadre, glissent sur les plaques de contact (balais).

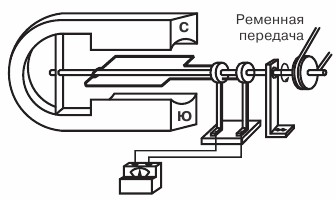
Figure 1. Schéma de l'alternateur le plus simple

Assurons-nous qu'un tel appareil est bien une source d'EMF variable.

Supposons qu'un aimant crée entre ses pôles champ magnétique uniforme, c'est-à-dire celui dans lequel la densité des lignes de champ magnétique dans chaque partie du champ est la même.tournant, le cadre croise les lignes de force du champ magnétique dans chacun de ses côtés a et b CEM induit. 

Les côtés c et d du cadre ne fonctionnent pas, car lorsque le cadre tourne, ils ne traversent pas les lignes de force du champ magnétique et ne participent donc pas à la création de l'EMF.

À tout instant, l'EMF se produisant du côté a est de direction opposée à l'EMF se produisant du côté b, mais dans le cadre, les deux EMF agissent en fonction et s'ajoutent à l'EMF total, c'est-à-dire induit par l'ensemble du cadre.

Ceci est facile à vérifier si nous utilisons la règle de la main droite que nous connaissons pour déterminer la direction de la FEM.

Pour ce faire, placez la paume de la main droite de manière à ce qu'elle soit face au pôle nord de l'aimant et que le pouce plié coïncide avec la direction du mouvement du côté du cadre dans lequel nous voulons déterminer la direction de l'EMF. Ensuite, la direction de l'EMF à l'intérieur sera indiquée par les doigts tendus de la main.

Quelle que soit la position du cadre, nous déterminons la direction de la FEM dans les côtés a et b, elles s'additionnent toujours et forment une FEM totale dans le cadre. Dans le même temps, à chaque rotation du cadre, la direction de la FEM totale dans celui-ci change dans le sens opposé, car chacun des côtés actifs du cadre en un tour passe sous différents pôles de l'aimant.

L'amplitude de la FEM induite dans le cadre change également à mesure que la vitesse à laquelle les côtés du cadre croisent les lignes de champ magnétique change. En effet, au moment où le cadre s'approche de sa position verticale et la dépasse, la vitesse de franchissement des lignes de force sur les côtés du cadre est la plus élevée, et la plus grande emf est induite dans le cadre.A ces instants, lorsque le cadre passe sa position horizontale, ses côtés semblent glisser le long des lignes de champ magnétique sans les croiser, et aucune force électromagnétique n'est induite.

Par conséquent, avec une rotation uniforme du cadre, une FEM y sera induite, changeant périodiquement à la fois en amplitude et en direction.

La FEM se produisant dans le cadre peut être mesurée par un appareil et utilisée pour créer un courant dans le circuit externe.

En utilisant phénomène d'induction électromagnétique, vous pouvez obtenir des champs électromagnétiques alternatifs et donc du courant alternatif.

Courant alternatif à usage industriel et pour l'éclairage produits par de puissants générateurs entraînés par des turbines à vapeur ou à eau et des moteurs à combustion interne.

Représentation graphique des courants AC et DC

La méthode graphique permet de visualiser le processus de modification d'une certaine variable en fonction du temps.

Le traçage des variables qui changent au fil du temps commence par tracer deux lignes mutuellement perpendiculaires appelées les axes du graphique. Ensuite, sur l'axe horizontal, sur une certaine échelle, les intervalles de temps sont tracés, et sur l'axe vertical, également sur une certaine échelle, les valeurs de la grandeur à tracer (EMF, tension ou courant).

En figue. 2 courant continu et courant alternatif représentés graphiquement ... Dans ce cas, nous retardons les valeurs de courant et les valeurs de courant d'une direction, généralement appelée positive, sont retardées verticalement à partir du point d'intersection des axes O , et vers le bas à partir de ce point, la direction opposée, qui est généralement appelée négative.

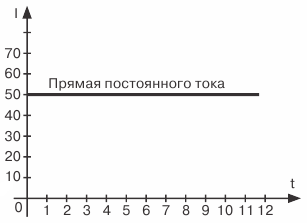
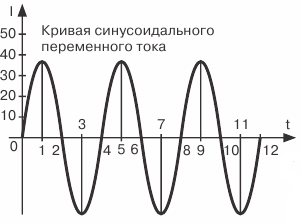Figure 2. Représentation graphique de DC et AC

Le point O lui-même sert à la fois d'origine des valeurs actuelles (verticalement vers le bas et vers le haut) et du temps (horizontalement vers la droite).En d'autres termes, ce point correspond à la valeur nulle du courant et à ce point de départ dans le temps à partir duquel on entend tracer l'évolution du courant dans le futur.

Vérifions l'exactitude de ce qui est tracé sur la fig. 2 et un tracé de courant continu de 50 mA.

Étant donné que ce courant est constant, c'est-à-dire qu'il ne change pas d'amplitude et de direction dans le temps, les mêmes valeurs de courant correspondront à différents moments, soit 50 mA. Ainsi, à l'instant de temps égal à zéro, c'est-à-dire à l'instant initial de notre observation du courant, il sera égal à 50 mA. En traçant un segment égal à la valeur actuelle de 50 mA sur l'axe vertical vers le haut, nous obtenons le premier point de notre graphique.

Il faut faire de même pour l'instant suivant correspondant au point 1 sur l'axe des temps, c'est-à-dire reporter de ce point verticalement vers le haut un segment également égal à 50 mA. La fin du segment définira pour nous le deuxième point du graphique.

Après avoir fait une construction similaire pour plusieurs points ultérieurs dans le temps, nous obtenons une série de points dont la connexion donnera une ligne droite, qui est une représentation graphique d'une valeur de courant constant de 50 mA.

Tracé d'une EMF variable

Passons à l'étude du graphique variable de l'EMF... Dans la fig. 3, un cadre tournant dans un champ magnétique est montré en haut, et une représentation graphique de la variable EMF résultante est donnée ci-dessous.

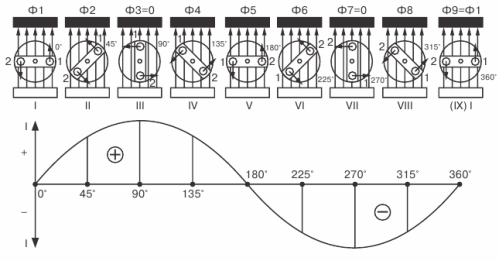Figure 3. Tracé de la variable EMF

Nous commençons à faire pivoter uniformément le cadre dans le sens des aiguilles d'une montre et à suivre l'évolution des changements EMF, en prenant la position horizontale du cadre comme moment initial.

À ce moment initial, la FEM sera nulle car les côtés du cadre ne croisent pas les lignes de champ magnétique.Sur le graphique, cette valeur nulle de FEM correspondant à l'instant t = 0 est représentée par le point 1.

Avec une rotation supplémentaire du cadre, l'EMF commencera à y apparaître et augmentera jusqu'à ce que le cadre atteigne sa position verticale. Sur le graphique, cette augmentation d'EMF sera représentée par une courbe ascendante lisse qui atteint son apogée (point 2).

Lorsque le cadre approche de la position horizontale, l'EMF qu'il contient diminue et tombe à zéro. Sur le graphique, cela sera représenté par une courbe lisse descendante.

Par conséquent, pendant le temps correspondant à un demi-tour du cadre, l'EMF dans celui-ci a pu augmenter de zéro à la valeur maximale et redescendre à zéro (point 3).

Avec une rotation supplémentaire du cadre, l'EMF y réapparaîtra et augmentera progressivement en amplitude, mais sa direction changera déjà dans le sens opposé, comme on peut le voir en appliquant la règle de la main droite.

Le graphique prend en compte le changement de direction de l'EMF, de sorte que la courbe représentant l'EMF croise l'axe du temps et se situe maintenant en dessous de cet axe. L'EMF augmente à nouveau jusqu'à ce que le cadre adopte une position verticale.

Ensuite, l'EMF commencera à diminuer et sa valeur deviendra égale à zéro lorsque le cadre reviendra à sa position d'origine après avoir effectué un tour complet. Sur le graphique, cela se traduira par le fait que la courbe EMF, atteignant son pic dans la direction opposée (point 4), rencontrera alors l'axe du temps (point 5)

Ceci termine un cycle de changement de l'EMF, mais si vous continuez la rotation du cadre, le deuxième cycle commence immédiatement, répétant exactement le premier, qui à son tour sera suivi du troisième, puis du quatrième, et ainsi de suite jusqu'à ce que nous nous arrêtions le cadre de rotation.

Ainsi, pour chaque rotation du cadre, la FEM qui s'y produit effectue un cycle complet de son changement.

Si le cadre est fermé à un circuit externe, un courant alternatif traversera le circuit, dont le graphique ressemblera au graphique EMF.

La forme d'onde résultante est appelée onde sinusoïdale, et le courant, la FEM ou la tension variant selon cette loi est appelé sinusoïdal.

La courbe elle-même est appelée sinusoïde car il s'agit d'une représentation graphique d'une grandeur trigonométrique variable appelée sinus.

La nature sinusoïdale du changement de courant est la plus courante en génie électrique, par conséquent, en parlant de courant alternatif, dans la plupart des cas, il s'agit de courant sinusoïdal.

Pour comparer différents courants alternatifs (FEM et tensions), il existe des valeurs qui caractérisent un certain courant. Ceux-ci sont appelés paramètres AC.

Période, Amplitude et Fréquence — Paramètres AC

Le courant alternatif est caractérisé par deux paramètres - cycle mensuel et amplitude, sachant que nous pouvons estimer de quel type de courant alternatif il s'agit et construire un graphique du courant.

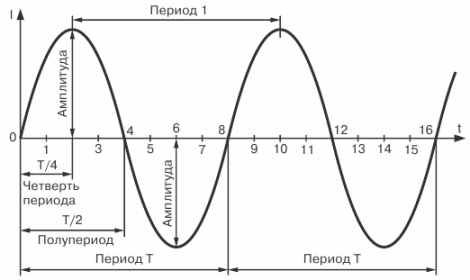
Figure 4. Courbe de courant sinusoïdale

La période de temps pendant laquelle un cycle complet de changement de courant se produit est appelée une période. La période est désignée par la lettre T et est mesurée en secondes.

La période de temps pendant laquelle la moitié d'un cycle complet de changement de courant se produit est appelée un demi-cycle.Par conséquent, la période de changement de courant (FEM ou tension) se compose de deux demi-périodes. Il est bien évident que toutes les périodes d'un même courant alternatif sont égales les unes aux autres.

Comme on peut le voir sur le graphique, pendant une période de son changement, le courant atteint deux fois sa valeur maximale.

La valeur maximale d'un courant alternatif (FEM ou tension) est appelée son amplitude ou valeur de courant de crête.

Im, Em et Um sont des désignations courantes pour les amplitudes de courant, de FEM et de tension.

Tout d'abord, nous avons fait attention courant de crête, cependant, comme on peut le voir sur le graphique, il existe d'innombrables valeurs intermédiaires inférieures à l'amplitude.

La valeur du courant alternatif (FEM, tension) correspondant à n'importe quel moment sélectionné dans le temps est appelée sa valeur instantanée.

i, e et u sont des désignations communément acceptées des valeurs instantanées du courant, de la force électromotrice et de la tension.

La valeur instantanée du courant, ainsi que sa valeur de crête, est facile à déterminer à l'aide du graphique. Pour ce faire, à partir de n'importe quel point de l'axe horizontal correspondant au moment qui nous intéresse, tracez une ligne verticale jusqu'au point d'intersection avec la courbe actuelle ; le segment résultant de la ligne verticale déterminera la valeur du courant à un instant donné, c'est-à-dire sa valeur instantanée.

Évidemment, la valeur instantanée du courant après l'instant T/2 depuis le point de départ du graphique sera nulle, et après l'instant T/4 sa valeur d'amplitude. Le courant atteint également sa valeur maximale ; mais déjà en sens inverse, après un temps égal à 3/4 T.

Ainsi, le graphique montre comment le courant dans le circuit change au fil du temps et qu'une seule valeur particulière de l'amplitude et de la direction du courant correspond à chaque instant de temps. Dans ce cas, la valeur du courant à un instant donné en un point du circuit sera exactement la même en tout autre point de ce circuit.

Il est appelé le nombre de périodes complètes remplies par le courant en 1 seconde de fréquence alternative et est désigné par la lettre latine f.

Pour déterminer la fréquence d'un courant alternatif, c'est-à-dire pour savoir combien de périodes de son changement le courant a fait en 1 seconde, il est nécessaire de diviser 1 seconde par le temps d'une période f = 1 / T. Connaissant la fréquence du courant alternatif, vous pouvez déterminer la période : T = 1 / f

Fréquence CA il est mesuré dans une unité appelée hertz.

Si nous avons un courant alternatif dont la fréquence est égale à 1 hertz, alors la période d'un tel courant sera égale à 1 seconde. A l'inverse, si la période de variation du courant est de 1 seconde, alors la fréquence d'un tel courant est de 1 hertz.

Nous avons donc défini des paramètres AC (période, amplitude et fréquence) qui vous permettent de faire la distinction entre différents courants AC, EMF et tensions, et de tracer leurs graphiques si nécessaire.

Lors de la détermination de la résistance de divers circuits au courant alternatif, utilisez une autre valeur auxiliaire caractérisant le courant alternatif, la soi-disant fréquence angulaire ou angulaire.

Fréquence circulaire notée liée à la fréquence f par le rapport 2 pif

Expliquons cette dépendance. Lors du traçage du graphique EMF variable, nous avons vu qu'une rotation complète du cadre se traduit par un cycle complet de changement EMF. En d'autres termes, pour que la monture fasse un tour, c'est-à-dire pour faire une rotation de 360°, il faut un temps égal à une période, soit T secondes. Puis, en 1 seconde, le châssis effectue une révolution de 360°/T. Par conséquent, 360 ° / T est l'angle de rotation du cadre en 1 seconde et exprime la vitesse de rotation du cadre, généralement appelée vitesse angulaire ou circulaire.

Mais puisque la période T est liée à la fréquence f par le rapport f = 1 / T, alors la vitesse circulaire peut aussi s'exprimer en fréquence et sera égale à 360°f.

Nous avons donc conclu que 360 ​​° f. Cependant, pour la commodité d'utiliser la fréquence circulaire pour tous les calculs, l'angle de 360 ​​​​° correspondant à un tour est remplacé par une expression radiale égale à 2pi radians, où pi = 3,14. Nous obtenons donc finalement 2pif. Par conséquent, pour déterminer la fréquence angulaire du courant alternatif (FEM ou tension), vous devez multiplier la fréquence en hertz par un nombre constant 6,28.