Oscillations continues et résonance paramétrique

Vibrations continues — vibrations dont l'énergie ne change pas dans le temps. Dans les systèmes physiques réels, il existe toujours des causes qui provoquent la transition de l'énergie vibratoire à l'énergie thermique (par exemple, le frottement dans les systèmes mécaniques, la résistance active dans les systèmes électriques).

Par conséquent, des oscillations non amorties ne peuvent être obtenues qu'à condition de reconstituer ces pertes d'énergie. Un tel réapprovisionnement se produit automatiquement dans les systèmes auto-oscillants en raison de l'énergie provenant d'une source externe. Les oscillations électromagnétiques continues sont extrêmement largement utilisées. Différents générateurs sont utilisés pour les obtenir.

Pour rendre non amorties les vibrations électriques ou mécaniques (d'un cercle oscillant ou d'un pendule), il est nécessaire de compenser en permanence les pertes par résistance ou par frottement.

Par exemple, vous pouvez agir sur le circuit oscillant avec une force électromotrice alternative, ce qui augmentera périodiquement le courant dans la bobine et, par conséquent, maintiendra l'amplitude de tension dans le condensateur.Ou vous pouvez pousser le pendule de la même manière, en le faisant osciller harmonieusement.

Comme vous le savez, l'amplitude de l'énergie du champ magnétique de la bobine du circuit oscillant est liée à son inductance et à son courant par la relation suivante (la deuxième formule esténergie du champ électrique du condensateur même contour contour)

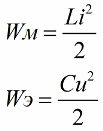
Il ressort clairement de la première formule que si nous augmentons périodiquement le courant dans la bobine, en agissant sur le circuit EMF alternatif, alors (en augmentant ou en diminuant le deuxième facteur de la formule - le courant), nous reconstituerons périodiquement ce circuit en énergie.

En agissant sur le circuit strictement dans le temps avec ses oscillations libres naturelles, c'est-à-dire à la fréquence de résonance, nous obtiendrons le phénomène de résonance électrique, car il est à la fréquence de résonance système oscillant absorbe le plus intensément l'énergie qui lui est fournie.

Mais que se passe-t-il si vous modifiez périodiquement non pas le deuxième facteur (pas de courant ni de tension), mais le premier facteur - l'inductance ou la capacité ? Dans ce cas, le circuit subira également une modification de son énergie.

Par exemple, pousser périodiquement le noyau dans et hors de la bobine ou pousser dans et hors du condensateurdiélectrique, - nous obtenons également un changement périodique très précis de l'énergie dans le circuit.

Nous écrivons cette position pour un changement d'unité dans l'inductance de la bobine :

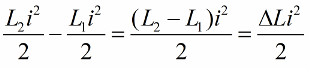
L'effet le plus prononcé de l'oscillation du circuit sera si les changements d'inductance sont effectués juste à temps. Par exemple, si nous prenons le même circuit à tout moment, lorsqu'un courant i le traverse déjà, et introduisons un noyau dans la bobine, l'énergie changera de la quantité suivante :

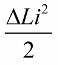
Laissez maintenant apparaître des oscillations libres dans le circuit lui-même, mais au moment où, après un quart de période, l'énergie est complètement passée dans le condensateur et le courant dans la bobine est devenu nul, nous allons retirer brusquement le noyau de la bobine L'inductance reviendra à son état d'origine, à la valeur initiale L. Aucun travail ne doit être effectué contre le champ magnétique lorsque le noyau est retiré. Par conséquent, lorsque le noyau a été poussé dans la bobine, le circuit a reçu de l'énergie, puisque nous avons travaillé, dont la valeur :

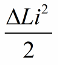
Après un quart de la période, le condensateur commence à se décharger, son énergie est à nouveau convertie en énergie du champ magnétique de la bobine.Lorsque le champ magnétique atteint l'amplitude, nous appuierons à nouveau fortement sur le noyau. Encore une fois, l'inductance a augmenté, augmentée du même montant.

Et encore une fois, à courant nul, nous ramenons l'inductance à sa valeur d'origine. En conséquence, si les gains d'énergie pour chaque demi-cycle dépassent les pertes de résistance, l'énergie de la boucle augmentera tout le temps et l'amplitude d'oscillation augmentera. Cette situation s'exprime par l'inégalité :

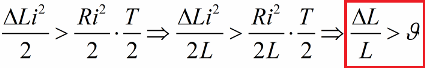
Ici, nous avons divisé les deux côtés de cette inégalité par L et noté la condition de possibilité d'excitation paramétrique par sauts pour une certaine valeur du décrément logarithmique.

Il est recommandé de changer l'inductance (ou la capacité) deux fois par période, donc la fréquence de changement de paramètre (fréquence de résonance paramétrique) doit être deux fois la fréquence propre du système oscillant :

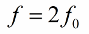
Ainsi, le chemin d'excitation des oscillations dans le circuit est apparu sans qu'il soit nécessaire de modifier directement la FEM ou le courant.Le courant fluctuant initial dans le circuit est toujours présent d'une manière ou d'une autre, et cela ne tient même pas compte des interférences des oscillations de radiofréquence dans l'atmosphère.

Si l'inductance (ou la capacité) ne change pas par sauts, mais harmoniquement, alors la condition d'apparition des oscillations sera un peu différente:

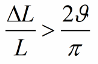
Étant donné que la capacité et l'inductance sont des paramètres de circuit (comme la masse d'un pendule ou l'élasticité d'un ressort), la méthode d'excitation des oscillations est également appelée excitation paramétrique.

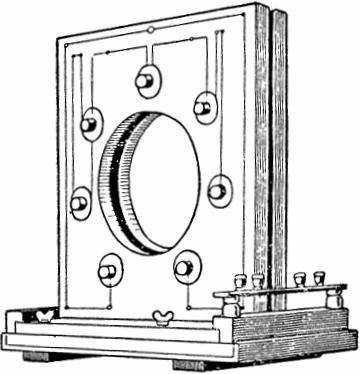
Ce phénomène a été découvert et pratiquement étudié au début du XXe siècle par les physiciens soviétiques Mandelstam et Papalexi. Sur la base de ce phénomène physique, ils ont construit le premier générateur de courant alternatif paramétrique d'une puissance de 4 kW et d'une inductance variable.

Dans la conception du générateur, sept paires de bobines plates étaient situées des deux côtés du cadre, dans la cavité desquelles un disque ferromagnétique avec des saillies tournait. Lorsque le disque est entraîné en rotation par un moteur, ses protubérances entrent et sortent périodiquement de l'espace entre chaque paire de bobines, modifiant ainsi l'inductance et provoquant des oscillations.