Théorie des automates, automates finis
La structure, la conception, le principe de fonctionnement de diverses machines sont largement déterminés par son objectif fonctionnel. Distinguer les machines technologiques, de transport, informatiques, militaires et autres. Des complexes automatiques entiers conçus pour effectuer des processus technologiques complexes sont largement introduits dans diverses industries. Les automates sont conçus et construits pour exécuter diverses fonctions logiques (machines logiques).
Théorie des automates — rubrique cybernétique, qui est né sous l'influence des exigences de la technologie des ordinateurs numériques et des machines de contrôle. Les automates discrets étudiés dans la théorie des automates sont des modèles abstraits de systèmes réels (à la fois techniques et biologiques) qui traitent des informations discrètes (numériques) à des pas de temps discrets.
La théorie des automates repose sur des concepts mathématiques précis qui formalisent des idées intuitives sur le fonctionnement (comportement) de l'automate et sur sa structure (structure interne).
Dans ce cas, la transformation d'informations est toujours comprise comme une opération qui transforme des séquences d'entrée composées de lettres de l'alphabet d'entrée en séquences de sortie composées de lettres de l'alphabet de sortie.
L'appareil de la logique mathématique, de l'algèbre, de la théorie des probabilités, de la combinatoire et de la théorie des graphes est largement utilisé.
Le problème avec la théorie des automates dans certaines de ses parties (théorie structurelle des automates) a grandi de la théorie des circuits relais-contact, qui a commencé à prendre forme à la fin des années 1930. compris méthodes d'algèbre logique.

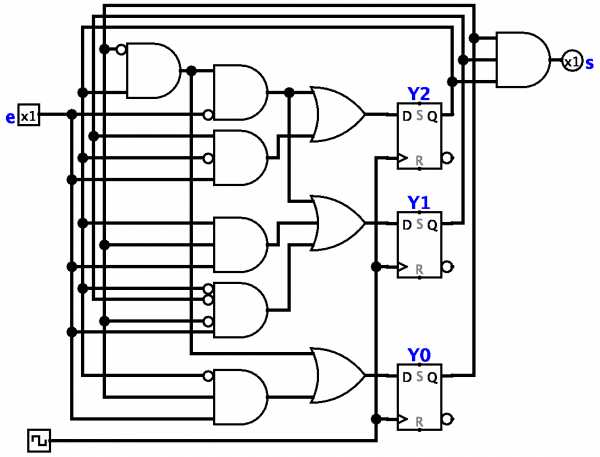
Dans la théorie structurelle des automates, différents types de schémas sont étudiés, conçus pour décrire comment un automate complexe est créé à partir de composants plus simples (éléments) correctement connectés dans un système.
Une autre direction, appelée la théorie abstraite des automates, étudie le comportement des automates (c'est-à-dire la nature de la transformation de l'information effectuée par eux), tout en faisant abstraction des spécificités de leur structure interne, et est née dans les années 1950.
Dans le cadre de la théorie abstraite des automates, le contenu des concepts « automate » et « machine » est essentiellement épuisé par la description standard de la transformation de l'information effectuée par un automate. Une telle transformation peut être déterministe, mais elle peut aussi être de nature probabiliste.
Les plus étudiées sont les machines déterministes (automates), qui comprennent des automates finis — le principal objet d'étude dans la théorie des automates.
Une machine à états finis est caractérisée par une quantité limitée de mémoire (le nombre d'états internes) et est définie à l'aide d'une fonction de transition.Avec une idéalisation raisonnable, toutes les machines mathématiques modernes et même le cerveau, du point de vue de leur fonctionnement, peuvent être considérés comme des automates finis.
Les termes « machine séquentielle », « automate de Milly », « automate de Moore » sont utilisés dans la littérature (et pas uniformément par tous les auteurs) comme synonymes du terme « automate fini » ou pour souligner certains traits dans les fonctions de transition d'un système fini. automate.
Les automates à mémoire illimitée sont une machine de Turing capable d'effectuer (potentiellement) n'importe quelle transformation efficace de l'information. Le concept de "machine de Turing" est apparu plus tôt que le concept de "machine à états finis" et est principalement étudié dans la théorie des algorithmes.
La théorie abstraite des automates est étroitement liée aux théories algébriques bien connues, par exemple la théorie des semi-groupes. D'un point de vue appliqué, les résultats caractérisant la transformation de l'information dans un automate en termes de taille mémoire sont intéressants.
C'est le cas, par exemple, dans les problèmes d'expériences sur les automates (travaux de E.F. Moore, etc.), où l'une ou l'autre information sur les fonctions de transition de l'automate ou sur la capacité de sa mémoire est obtenue à partir des résultats de la expériences.
Une autre tâche consiste à calculer les périodes des séquences de sortie, sur la base des informations disponibles sur la taille de la mémoire de l'automate et les périodes des séquences d'entrée.
Le développement de méthodes pour minimiser la mémoire des machines à états finis et étudier leur comportement dans des environnements aléatoires est d'une grande importance.
Dans la théorie abstraite des automates, le problème de synthèse est le suivant.En termes de langage clairement formalisé, les conditions sont écrites pour le comportement de l'automate conçu (pour l'événement représenté dans l'automate). Dans ce cas, il est nécessaire de développer des méthodes qui selon chaque condition écrite :
1) rechercher s'il existe une machine à états telle que les informations transformées par celle-ci remplissent cette condition ;
2) si oui, alors les fonctions de transition d'une telle machine à états finis sont construites ou sa taille mémoire est estimée.
La solution de la tâche de synthèse dans une telle formulation suppose la création préalable d'un langage commode pour enregistrer les conditions de fonctionnement d'un automate avec des algorithmes commodes pour le passage de l'enregistrement aux fonctions transitives.
Dans la théorie structurale des automates, le problème de synthèse consiste à construire une chaîne d'éléments d'un type donné qui réalise un automate fini donné par ses fonctions de transition. Dans ce cas, ils énoncent généralement un critère d'optimalité (par exemple, le nombre minimum d'éléments) et cherchent à obtenir un schéma optimal.
Comme il s'est avéré plus tard, cela signifie que certaines des méthodes et des concepts développés précédemment en relation avec les circuits à contacts de relais sont applicables à des circuits d'un autre type.
Dans le cadre du développement des technologies électroniques, les plus répandus sont les schémas d'éléments fonctionnels (réseaux logiques). Un cas particulier des réseaux logiques sont les réseaux de neurones abstraits, dont les éléments sont appelés neurones.
De nombreuses méthodes de synthèse ont été développées, selon le type de circuits et la transformation d'informations auxquelles ils sont destinés (Synthèse de dispositifs relais).
Regarder -Minimisation des circuits combinatoires, cartes de Carnot, synthèse de circuits
Machine à états finis — un modèle mathématique d'un système de commande avec une taille de mémoire fixe (incapable d'augmenter pendant le fonctionnement).
Le concept d'une machine à états finis est une abstraction mathématique qui caractérise les caractéristiques générales d'un ensemble de systèmes de contrôle (par exemple, un dispositif de relais multi-boucles). Tous ces systèmes ont des caractéristiques communes qu'il est naturel d'accepter comme définition d'un automate fini.
Chaque automate achevé a une entrée exposée aux influences extérieures et aux éléments intérieurs. Pour les éléments d'entrée et internes, il existe un nombre fixe d'états discrets qu'ils peuvent prendre.
Le changement d'état des éléments d'entrée et internes se produit à des moments discrets dans le temps, les intervalles entre lesquels sont appelés ticks. L'état interne (l'état des composants internes) à la fin de la bande est entièrement déterminé par l'état interne et l'état de l'entrée au début de la bande.
Toutes les autres définitions d'un automate fini peuvent être réduites à cette caractéristique, en particulier les définitions qui supposent qu'un automate fini a une sortie qui dépend de l'état interne de l'automate à un instant donné.
En termes d'une telle caractéristique, la nature de ses entrées et de ses états internes n'est pas pertinente pour la description d'un automate complet. Au lieu d'entrées et d'états, vous pouvez simplement regarder leurs numéros dans une numérotation aléatoire.
La machine d'état sera définie si la dépendance de son numéro d'état interne par rapport au numéro d'état interne précédent et au numéro d'état d'entrée précédent est spécifiée. Une telle tâche peut prendre la forme d'un tableau final.
Une autre façon courante de définir un automate complet est la construction de ce que l'on appelle diagrammes de transition. Les états d'entrée sont souvent appelés simplement des entrées et les états internes sont simplement des états.
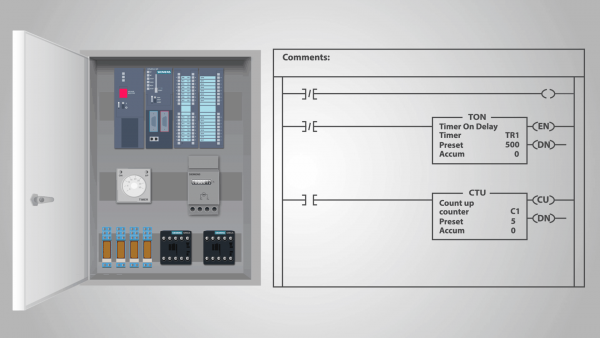
Une machine à états finis peut être un modèle à la fois de dispositifs techniques et de certains systèmes biologiques. Les automates du premier type sont, par exemple, des dispositifs de relais et divers ordinateurs électroniques, incl. contrôleurs logiques programmables.
Dans le cas d'un dispositif relais, le rôle d'états d'entrée est joué par des combinaisons d'états des éléments sensibles du dispositif relais (chaque combinaison de tels états est un « état complexe », caractérisé par une indication de tous les éléments sensibles de ces états discrets qu'ils ont à un instant donné). De même, des combinaisons d'états d'éléments intermédiaires d'un dispositif relais agissent comme des états internes.
Un contrôleur logique programmable (PLC) est un exemple de dispositif d'action de relais qui peut être appelé une machine d'état autonome.
En effet, une fois que le programme a été entré dans l'automate et que le contrôleur a commencé à calculer, il n'est pas exposé aux influences extérieures et chaque état suivant est entièrement déterminé par son état précédent. On peut supposer que l'entrée a le même état à chaque cycle d'horloge.
Inversement, toute machine à états finis qui possède le seul état d'entrée possible est naturellement dite autonome, puisque dans ce cas l'environnement externe ne porte aucune information qui contrôle son comportement.
Voir également: