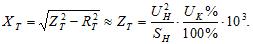Circuits de rechange pour transformateurs dans le calcul des réseaux électriques

De par la nature des tâches à résoudre, les calculs de réseaux électriques sont divisés en deux parties :

1. Calculs des modes réseau. Ce sont des calculs de tensions aux points nodaux, de courants et de puissances dans les lignes et les transformateurs à certains intervalles.

2. Calculs de sélection des paramètres. Ce sont des calculs de la sélection des tensions, des paramètres des lignes, des transformateurs, des dispositifs de compensation et autres.

Pour effectuer les calculs ci-dessus, vous devez d'abord connaître les circuits équivalents, la résistance et la conductance des lignes électriques et des transformateurs.

Dans les calculs des réseaux électriques, en tenant compte des transformateurs, au lieu du circuit équivalent en forme de T connu du cours de génie électrique, le circuit équivalent en forme de L le plus simple est généralement utilisé, ce qui simplifie grandement les calculs et ne provoque pas d'erreurs importantes . Un tel circuit équivalent est représenté sur la Fig. 1.

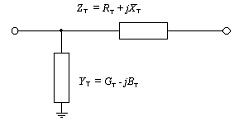
Riz. 1. Circuit équivalent de transformateur en forme de L

Les principaux paramètres du circuit équivalent d'une phase du transformateur sont la résistance active RT, réactivité HT, conductance active GT et conductance réactive BT. La conductance réactive de VT est de nature inductive. Ces paramètres sont absents de la littérature de référence. Elles sont déterminées expérimentalement selon les données du passeport : pertes à vide ∆PX, pertes sur court-circuit DRK, tension de court-circuit UK% et courant à vide i0%.

Pour les transformateurs à trois enroulements ou autotransformateurs, le circuit équivalent est présenté sous une forme légèrement différente (Fig. 2).

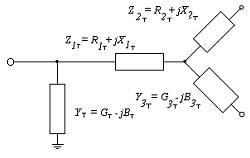
Riz. 2. Circuit équivalent d'un transformateur à trois enroulements

Dans les données de passeport des transformateurs à trois enroulements, la tension de court-circuit est indiquée pour trois combinaisons possibles : UK1-2 % en court-circuit sur l'enroulement moyenne tension (MT) et le côté alimentation de l'enroulement haute tension (HT) ; UK1-3% - en cas de court-circuit de l'enroulement basse tension (BT) et de l'alimentation électrique de l'enroulement HT ; UK2-3% — en cas de court-circuit de la bobine BT et de l'alimentation côté HT.

De plus, des versions du transformateur sont possibles lorsque les trois enroulements sont conçus pour la puissance nominale du transformateur ou lorsqu'un ou les deux enroulements secondaires sont conçus (en termes de chauffage) pour seulement 67 % de la puissance de l'enroulement primaire.

Les conductivités active et réactive du circuit équivalent sont déterminées par les formules :

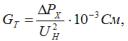
où ∆PX — en kW, UN — en kW.

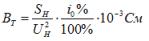
La résistance active totale des enroulements RTotot est calculée par la formule :

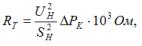
Si les trois enroulements sont conçus pour la pleine puissance, la résistance active de chacun d'eux est prise égale :

R1T = R2T = R3T = 0,5 RT total

Si l'un des enroulements secondaires est conçu pour 67% de la puissance, alors les résistances des enroulements pouvant être chargés à 100% sont prises égales à 0,5 RTotal. Une bobine qui permet de transmettre 67% de la puissance et dont la section est à 67% de la normale a une résistance 1,5 fois supérieure, soit 0,75 RTotot.

Pour déterminer la résistance de chacune des poutres, les circuits équivalents de la tension de court-circuit sont présentés comme la somme des chutes de tension relatives sur les poutres individuelles :

Royaume-Uni1-2 % = Royaume-Uni1 % + Royaume-Uni2 %,

Royaume-Uni1-3 % = Royaume-Uni1 % + Royaume-Uni3 %,

Royaume-Uni2-3 % = Royaume-Uni2 % + Royaume-Uni3 %.

En résolvant ce système d'équations pour UK1% et UK3%, on obtient :

Royaume-Uni1 % = 0,5 (Royaume-Uni1-2 % + Royaume-Uni1-3 %-Royaume-Uni2-3 %),

Royaume-Uni2 % = Royaume-Uni1-2 % + Royaume-Uni1 %,

Royaume-Uni3 % = Royaume-Uni1-3 % + Royaume-Uni1 %.

Dans les calculs pratiques pour l'un des faisceaux, la chute de tension est généralement nulle ou une petite valeur négative. Pour cette poutre du circuit équivalent, la résistance inductive est supposée nulle, et pour les poutres restantes, les réactances inductives sont trouvées en fonction des chutes de tension relatives par la formule :