Pertes et chutes de tension - quelles sont les différences

Dans la vie humaine ordinaire, les mots «perte» et «chute» sont utilisés pour désigner le fait d'une diminution de certaines réalisations, mais ils signifient une valeur différente.

Dans ce cas, «pertes» signifie perte d'une pièce, endommagement, réduction de la taille du niveau précédemment atteint. Les pertes ne sont pas souhaitables, mais vous pouvez les tolérer.

Le mot "chute" est compris comme un préjudice plus grave associé à une privation totale de droits. Ainsi, même des pertes occasionnelles (par exemple, un portefeuille) au fil du temps peuvent entraîner une baisse (par exemple, le niveau de vie matérielle).

À cet égard, nous examinerons cette question par rapport à la tension du réseau électrique.

Comment se forment les pertes et les chutes de tension

L'électricité est transportée sur de longues distances par des lignes aériennes d'une sous-station à une autre.

Les lignes aériennes sont conçues pour transmettre la puissance admissible et sont constituées de fils métalliques d'un certain matériau et d'une certaine section. Ils créent une charge résistive avec une valeur de résistance de R et une charge réactive de X.

Du côté de la réception, il se tient transformateurtransformation électrique.Ses bobines ont une résistance inductive XL active et prononcée. Le côté secondaire du transformateur abaisse la tension et la transmet ensuite aux consommateurs, dont la charge est exprimée par la valeur de Z et est de nature active, capacitive et inductive. Cela affecte également les paramètres électriques du réseau.

La tension appliquée aux fils du support de la ligne aérienne, la plus proche de la sous-station de transport d'énergie, surmonte la résistance réactive et active du circuit dans chaque phase et y crée un courant dont le vecteur s'écarte du vecteur de la tension appliquée d'un angle φ.

La nature de la distribution des tensions et du flux des courants le long de la ligne pour un mode de charge symétrique est illustrée sur la photo.

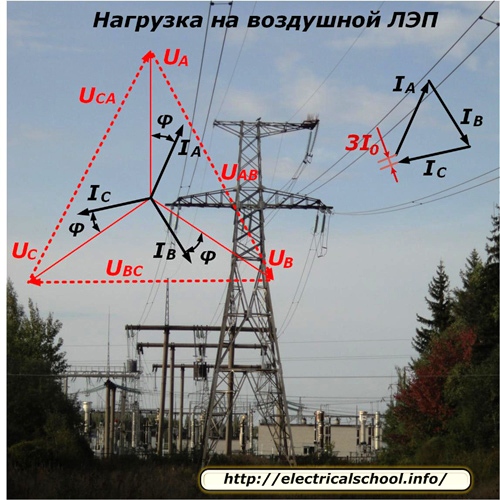
Étant donné que chaque phase de la ligne alimente un nombre différent de consommateurs qui sont également déconnectés ou connectés au travail de manière aléatoire, il est techniquement très difficile d'équilibrer parfaitement la charge des phases. Il y a toujours un déséquilibre dans celui-ci, qui est déterminé par l'addition vectorielle des courants de phase et écrit 3I0. Dans la plupart des calculs, il est simplement ignoré.

L'énergie consommée par la sous-station émettrice est en partie dépensée pour surmonter la résistance de la ligne et atteint le côté récepteur avec peu de changement. Cette fraction est caractérisée par une perte et une chute de tension dont le vecteur diminue légèrement en amplitude et se décale d'un angle à chaque phase.

Comment les pertes et les chutes de tension sont calculées

Afin de comprendre les processus qui se déroulent lors de la transmission de l'électricité, la forme vectorielle est pratique pour représenter les principales caractéristiques. Diverses méthodes de calcul mathématique sont également basées sur cette méthode.

Pour simplifier les calculs en système triphasé il est représenté par trois circuits équivalents monophasés. Cette méthode fonctionne bien avec une charge symétrique et permet d'analyser les processus lorsqu'elle est rompue.

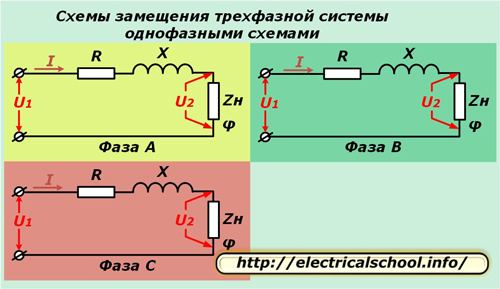
Dans les schémas ci-dessus, l'actif R et la réactance X de chaque conducteur de la ligne sont connectés en série avec la résistance de charge complexe Zn caractérisée par l'angle φ.

De plus, le calcul de la perte de tension et de la chute de tension dans une phase est effectué. Pour ce faire, vous devez spécifier les données. À cette fin, une sous-station est sélectionnée qui reçoit de l'énergie, où la charge admissible doit déjà être déterminée.

La valeur de tension de tout système à haute tension est déjà indiquée dans les ouvrages de référence et les résistances des fils sont déterminées par leur longueur, leur section, leur matériau et la configuration du réseau. Le courant maximum dans le circuit est défini et limité par les propriétés des fils.

Donc, pour commencer les calculs, nous avons : U2, R, X, Z, I, φ.

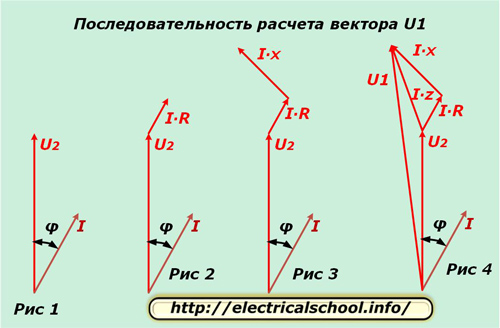
Nous prenons une phase, par exemple, «A» et séparons pour elle dans le plan complexe les vecteurs U2 et I, déplacés d'un angle φ, comme indiqué sur la figure 1. La différence de potentiel dans la résistance active du conducteur coïncide dans la direction avec le courant et en magnitude est déterminé à partir de l'expression I ∙ R. On reporte ce vecteur de la fin de U2 (Fig. 2).

La différence de potentiel dans la réactance du conducteur diffère de la direction du courant d'un angle φ1 et est calculée à partir du produit I ∙ X. Nous la reportons à partir du vecteur I ∙ R (Fig. 3).

Rappels : pour le sens positif de rotation des vecteurs dans le plan complexe, on prend le mouvement anti-horaire. Le courant traversant la charge inductive est en retard d'un angle sur la tension appliquée.

La figure 4 montre le tracé des vecteurs de différence de potentiel sur la résistance totale du fil I ∙ Z et la tension à l'entrée du circuit U1.

Vous pouvez maintenant comparer les vecteurs d'entrée au circuit équivalent et à travers la charge. Pour ce faire, placez le diagramme résultant horizontalement (Fig. 5) et tracez un arc depuis le début avec le rayon du module U1 jusqu'à ce qu'il croise la direction du vecteur U2 (Fig. 6).

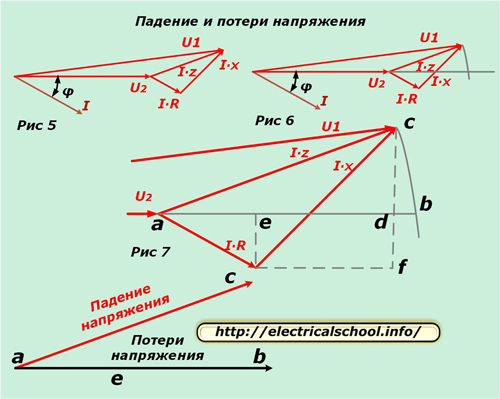
La figure 7 montre un agrandissement du triangle pour plus de clarté et le dessin de lignes auxiliaires, indiquant les points d'intersection caractéristiques avec des lettres.

Au bas de l'image, il est indiqué que le vecteur résultant ac est appelé la chute de tension et ab est appelé la perte. Ils diffèrent par leur taille et leur direction. Si nous revenons à l'échelle d'origine, nous verrons que ac est obtenu à la suite de la soustraction géométrique de vecteurs (U2 de U1), et ab est arithmétique. Ce processus est illustré dans l'image ci-dessous (Fig. 8).

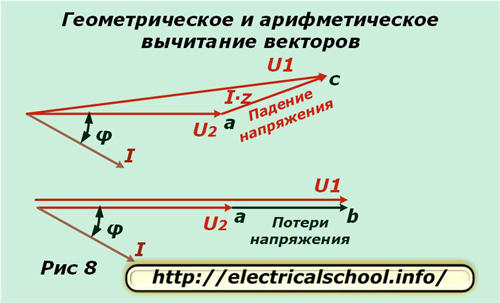
Dérivation des formules de calcul des pertes de tension

Revenons maintenant à la figure 7 et remarquons que le segment bd est très petit. Pour cette raison, elle est négligée dans les calculs et la perte de tension est calculée à partir de la longueur de segment ad. Il se compose de deux segments de droite ae et ed.

Puisque ae = I ∙ R ∙ cosφ et ed = I ∙ x ∙ sinφ, alors la perte de tension pour une phase peut être calculée par la formule :

∆Uph = je ∙ R ∙ cosφ + je ∙ x ∙ sinφ

Si nous supposons que la charge est symétrique dans toutes les phases (en négligeant conditionnellement 3I0), nous pouvons utiliser des méthodes mathématiques pour calculer la perte de tension dans la ligne.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Si le côté droit de cette formule est multiplié et divisé par la tension du réseau Un, nous obtenons alors une formule qui nous permet d'effectuer pCalcul des pertes de tension via l'alimentation.

∆Ul = (P ∙ r + Q ∙ x) / Un

Les valeurs de puissance active P et réactive Q peuvent être extraites des relevés des compteurs de ligne.

Ainsi, la perte de tension dans un circuit électrique dépend :

• active et réactance du circuit ;

• composants de la puissance appliquée ;

• l'amplitude de la tension appliquée.

Dérivation des formules de calcul de la composante transverse de la chute de tension

Revenons à la figure 7. La valeur du vecteur ac peut être représentée par l'hypoténuse d'un triangle rectangle acd. Nous avons déjà calculé le pied publicitaire. Déterminons la composante transverse cd.

La figure montre que cd = cf-df.

df = ce = je ∙ R ∙ sin φ.

cf = je ∙ x ∙ cos φ.

cd = je ∙ x ∙ cosφ-je ∙ R ∙ sinφ.

En utilisant les modèles obtenus, nous effectuons de petites transformations mathématiques et obtenons la composante transverse de la chute de tension.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Détermination de la formule de calcul de la tension U1 au début de la ligne électrique

Connaissant la valeur de la tension en bout de ligne U2, la perte ∆Ul et la composante transverse de la chute δU, on peut calculer la valeur du vecteur U1 par le théorème de Pythagore. Sous forme développée, il a la forme suivante.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Utilisation pratique

Le calcul des pertes de tension est effectué par des ingénieurs au stade de la création d'un projet de circuit électrique pour la sélection optimale de la configuration du réseau et de ses éléments constitutifs.

Pendant le fonctionnement des installations électriques, si nécessaire, des mesures simultanées des vecteurs de tension aux extrémités des lignes peuvent être effectuées périodiquement et les résultats obtenus par la méthode des calculs simples peuvent être comparés.Cette méthode convient aux appareils qui ont augmenté exigences en raison de la nécessité d'une grande précision de travail.

Pertes de tension dans les circuits secondaires

Un exemple est les circuits secondaires des transformateurs de tension de mesure, qui atteignent parfois plusieurs centaines de mètres de longueur et sont transmis par un câble d'alimentation spécial avec une section accrue.

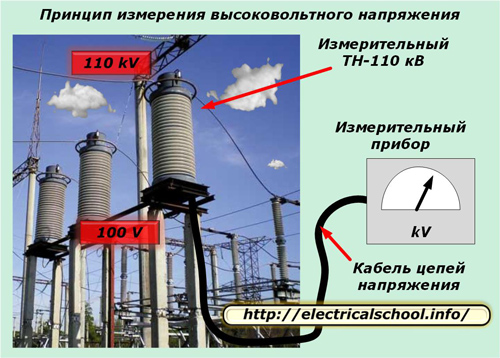
Les caractéristiques électriques d'un tel câble sont soumises à des exigences accrues en matière de qualité de transmission de tension.

La protection moderne des équipements électriques nécessite le fonctionnement de systèmes de mesure avec des indicateurs métrologiques élevés et une classe de précision de 0,5 voire 0,2. Par conséquent, les pertes de tension qui leur sont appliquées doivent être surveillées et prises en compte. Sinon, l'erreur introduite par eux dans le fonctionnement de l'équipement peut affecter de manière significative toutes les caractéristiques opérationnelles.

Pertes de tension dans les longues lignes de câble

La caractéristique de la conception du câble long est qu'il a une résistance capacitive en raison de la disposition assez proche des âmes conductrices et d'une fine couche d'isolation entre elles. Il dévie en outre le vecteur de courant traversant le câble et modifie son amplitude.

L'effet de la chute de tension sur la résistance capacitive doit être pris en compte dans le calcul pour modifier la valeur de I ∙ z. Sinon, la technologie décrite ci-dessus ne change pas.

L'article fournit des exemples de pertes et de chutes de tension sur les lignes électriques aériennes et les câbles. Cependant, on les trouve dans tous les consommateurs d'électricité, y compris les moteurs électriques, les transformateurs, les inductances, les batteries de condensateurs et autres appareils.

La quantité de pertes de tension pour chaque type d'équipement électrique est légalement réglementée en termes de conditions de fonctionnement, et le principe de leur détermination dans tous les circuits électriques est le même.