Résistances, conductances et circuits équivalents des transformateurs et autotransformateurs

Un transformateur à deux enroulements peut être représenté par un circuit équivalent en forme de T (Fig.1, a), où rt et xt sont la résistance active et inductive des enroulements, gt est la conductivité active due à la perte de puissance active dans le transformateur acier, bt est la conduction inductive due au courant magnétisant...

Le courant dans la conduction du transformateur est très faible (de l'ordre de quelques pour cent de son courant nominal), par conséquent, lors du calcul des réseaux électriques d'importance régionale, un circuit équivalent avec un transformateur en forme de L est généralement utilisé, dans lequel la conduction est ajoutée aux bornes de l'enroulement primaire du transformateur (Fig. 1, b) - à l'enroulement haute tension pour les transformateurs abaisseurs et à l'enroulement basse tension pour les transformateurs élévateurs. L'utilisation d'un schéma en forme de L simplifie les calculs des réseaux électriques.

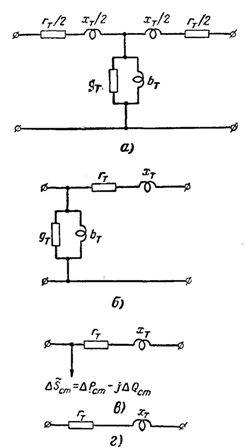
Riz. 1.Circuits équivalents d'un transformateur à deux enroulements : circuit en forme de T ; b — schéma en forme de G ; c — schéma simplifié en forme de L pour le calcul des réseaux régionaux ; d — un schéma simplifié pour le calcul des réseaux locaux et pour le calcul approximatif des réseaux régionaux.

Le calcul est encore plus simple si la conductivité du transformateur est remplacée par une charge constante (Fig.1, c) égale à la puissance à vide du transformateur :

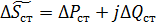
Ici ΔPCT — pertes de puissance dans l'acier égales aux pertes pendant le fonctionnement à vide du transformateur, et ΔQST — puissance magnétisante du transformateur égale à :

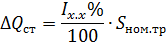
où Ix.x% est le courant à vide du transformateur en pourcentage de son courant nominal ; Snom.tr — puissance nominale du transformateur.

Pour les réseaux locaux n, dans les calculs approximatifs des réseaux régionaux, seules les résistances active et inductive des transformateurs sont généralement prises en compte (Fig. 1, d).

La résistance active des enroulements d'un transformateur à deux enroulements est déterminée par les pertes de puissance connues dans le cuivre (dans les enroulements) du transformateur ΔPm kW à sa charge nominale :

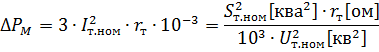
où

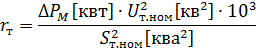
Dans les calculs pratiques, on suppose que les pertes de puissance dans le cuivre (dans les enroulements) d'un transformateur à sa charge nominale sont égales aux pertes de court-circuit au courant nominal du transformateur, c'est-à-dire ΔPm ≈ ΔPk.

Connaissant la tension de court-circuit uk% du transformateur, numériquement égale à la chute de tension dans ses enroulements à charge nominale, exprimée en pourcentage de sa tension nominale, c'est-à-dire

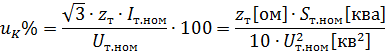
l'impédance des enroulements du transformateur peut être déterminée

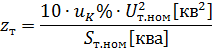
puis la résistance inductive des enroulements du transformateur

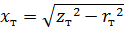
Pour les gros transformateurs à très faible résistance, la résistance inductive est généralement donnée par la condition approximative suivante :

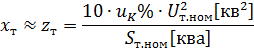
Lors de l'utilisation des formules de calcul, il convient de garder à l'esprit que les résistances des enroulements du transformateur peuvent être déterminées à la tension nominale de ses enroulements primaire et secondaire. Dans les calculs pratiques, il est plus pratique de déterminer rt et xt à la tension nominale de l'enroulement pour lequel le calcul est effectué.

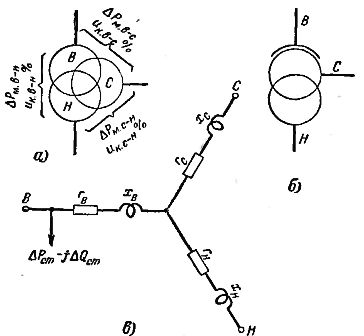
Riz. 2... Circuits de transformateurs à trois enroulements et autotransformateurs : a — schéma d'un transformateur à trois enroulements ; b - circuit autotransformateur ; c - circuit équivalent d'un transformateur à trois enroulements et d'un autotransformateur.

Si l'enroulement du transformateur a un nombre de tours réglable, alors Ut.nom est pris comme sortie de l'enroulement principal.

Les transformateurs à trois enroulements (Fig. 2, a) et les autotransformateurs (Fig. 2, b) sont caractérisés par les valeurs des pertes de puissance ΔРm = ΔРк. et les tensions de court-circuit ir% pour chaque paire d'enroulements :

ΔPk. c-s, ΔPk. vn, ΔPk. s-n

et

ik.v-s, ℅, ik.v-n, ℅, ik. s-n, ℅,

réduite à la puissance nominale du transformateur ou de l'autotransformateur. La puissance nominale de ce dernier est égale à sa puissance passante. Le circuit équivalent d'un transformateur ou d'un autotransformateur à trois enroulements est illustré à la Fig. 2, v.

Les pertes de puissance et la tension de court-circuit relatives aux rayons individuels d'une étoile équivalente d'un circuit équivalent sont déterminées par les formules :

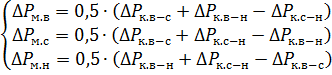
et

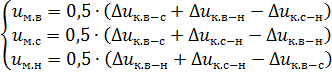
La résistance active et inductive des rayons de l'étoile équivalente du circuit équivalent est déterminée à partir des formules des transformateurs à deux enroulements, en y substituant les valeurs de perte de puissance et de tension de court-circuit pour le rayon correspondant de l'étoile équivalente du circuit équivalent.