Forces électrodynamiques dans les parties actives des structures et des dispositifs

Les parties des équipements électriques et des dispositifs de distribution sous tension, lorsqu'elles sont parcourues par du courant, sont exposées à des forces électrodynamiques... Comme vous le savez, de telles forces agissent sur tout conducteur porteur de courant situé dans champ magnétique.

Les grandeurs de ces efforts pour les éléments de l'appareillage et les appareils de configuration simple peuvent être déterminées à partir de la loi de Biot-Savard :

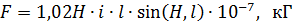
où (H, l) est l'angle formé par la direction du courant et la direction du champ magnétique ; avec des fils parallèles est de 90°.

Si deux conducteurs parallèles se déplacent dans un courant et qu'un conducteur avec un courant i1 est dans un champ magnétique avec un courant i2 d'intensité H = 0,2 • i2 / a, alors l'amplitude de la force agissant entre eux sera égale à

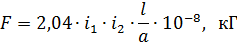
où i1 et i2 sont les courants des premier et deuxième fils, et ; a est la distance entre les axes des fils, cm; l — longueur du fil, voir

La force agissant entre les fils les attire les uns vers les autres avec le même sens de courant et les repousse dans des directions différentes.

La plus grande valeur de ces forces électrodynamiques est déterminée par le courant de court-circuit maximal possible, c'est-à-dire le courant de court-circuit iy. Par conséquent, le moment initial du court-circuit (t = 0,01 s) est le plus dangereux en termes d'amplitude des forces dynamiques.

Lorsqu'un courant de court-circuit traverse le disjoncteur ou lorsqu'il est connecté à un réseau existant court-circuit ses parties individuelles — traversées, tiges conductrices, traverses, tiges, etc., ainsi que les pneus et barres omnibus correspondants — sont soumis à une charge mécanique soudaine, qui a le caractère d'un choc.

Dans les systèmes électriques modernes de haute puissance à des tensions de 6 à 20 kV, les courants de court-circuit peuvent atteindre des valeurs allant jusqu'à 200 à 300 ka et plus, tandis que les forces électrodynamiques atteignent plusieurs tonnes par bus (ou bus) de 1 à 1,5 m de long. ...

Dans de telles conditions, la résistance mécanique insuffisante de l'un ou l'autre élément de l'équipement électrique peut entraîner une évolution ultérieure de l'accident et provoquer de graves dommages à l'appareillage. Par conséquent, pour le fonctionnement fiable de toute installation électrique, tous ses éléments doivent avoir une stabilité électrodynamique (résistance mécanique adéquate), c'est-à-dire résister aux effets d'un court-circuit.

Lors de la détermination des forces électrodynamiques selon la formule ci-dessus, on suppose que le courant circule le long de l'axe des fils ronds, dont le diamètre n'affecte pas l'amplitude des forces. Il convient de noter que la taille et la forme de la section transversale des fils à de grandes distances entre eux n'ont aucun effet notable sur l'amplitude des forces électrodynamiques.

Si les fils se présentent sous la forme de bandes rectangulaires et sont situés à une faible distance les uns des autres, lorsque la distance dans la lumière est inférieure au périmètre de la bande, les dimensions de leur section peuvent avoir une influence significative sur les forces électrodynamiques. Cette influence des dimensions de la section du conducteur est prise en compte dans les calculs utilisant le facteur de forme.

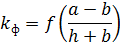
Si fils sous tension appartiennent au même circuit et i1 = i2 = iy alors la plus grande force d'interaction sera égale à

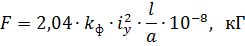
Avec diverses autres formes de fils simples et complexes, il est plus pratique d'utiliser le principe de l'augmentation de l'énergie électromagnétique et des dépendances qui en résultent.

De telles dépendances simples peuvent être obtenues en considérant deux circuits en interaction L1 et L2 portés par les courants i1 et i2. L'alimentation en énergie électromagnétique de ces circuits sera la suivante :

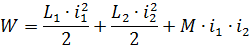
Si, à la suite de l'interaction des courants i1 et i2, la boucle du système est déformée sous l'action de forces électrodynamiques dans n'importe quelle direction de la quantité dx, alors le travail effectué par l'intensité du champ Fx sera égal à l'augmentation dans la fourniture d'énergie électromagnétique au système par la quantité dW :

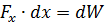
où:

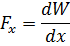
Dans les cas où, en pratique, il est nécessaire de déterminer la force électrodynamique entre des parties ou des côtés d'un même circuit avec une inductance L1-L, la force d'interaction sera :

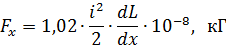
En utilisant cette expression, nous déterminons les forces électrodynamiques pour plusieurs cas simples mais pratiquement importants :

1. Fils parallèles avec un cavalier.

Dans les disjoncteurs et sectionneurs à huile, un circuit est formé avec cette configuration.

L'inductance de la boucle sera

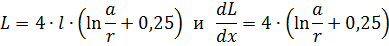
donc la force agissant sur la cloison est

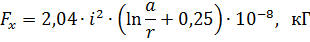
où a est la distance entre les axes des fils ; r est le rayon du fil.

Cette expression donne les forces électrodynamiques agissant sur le faisceau ou la lame de l'aiguillage. Ils facilitent le mouvement de la course du disjoncteur d'huile lorsque le courant est coupé et le repoussent lorsqu'il est allumé.

Pour avoir une idée de l'amplitude des forces résultantes, il suffit de dire que, par exemple, dans le disjoncteur de puissance VMB-10 avec un courant de court-circuit de 50 kA, la force agissant sur la traverse est d'environ 200 kg.

2. Un conducteur plié à angle droit.

Un tel agencement de conducteurs est habituellement utilisé dans les appareillages pour agencer les jeux de barres des approches vers et après l'appareillage, on le retrouve également dans les sectionneurs de traversée.

L'inductance du conducteur formant un tel circuit sera :

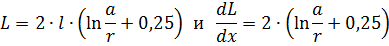
Par conséquent, l'effort du site sera déterminé comme dans le cas précédent :

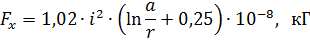
où a est la longueur d'un élément mobile, par exemple une lame de sectionneur.

Sous l'action du courant, le fil plié en biais a tendance à se redresser, et si un côté de celui-ci est mobile, par exemple, la lame du sectionneur, alors des mesures doivent être prises contre un éventuel déclenchement spontané lors d'un court-circuit.