Résonance des courants

Connexion en parallèle d'un condensateur et d'une inductance dans un circuit à courant alternatif

Considérez les phénomènes dans la chaîne courant alternatifcontenant un générateur, un condensateur et une inductance connectés en parallèle. Supposons que le circuit n'a pas de résistance active.

Évidemment, dans un tel circuit, la tension de la bobine et du condensateur est à tout moment égale à la tension développée par le générateur.

Le courant total dans un circuit est constitué des courants dans ses branches. Le courant dans la branche inductive est en retard sur la tension en phase d'un quart de période, et le courant dans la branche capacitive l'avance du même quart de période. Par conséquent, les courants dans les branches à tout instant se révèlent déphasés les uns par rapport aux autres d'une demi-période, c'est-à-dire qu'ils sont en opposition de phase. Ainsi, les courants dans les branches sont à tout moment dirigés les uns vers les autres et le courant total dans la partie non ramifiée du circuit est égal à leur différence.

Ceci nous donne le droit d'écrire l'égalité I = IL -circuit intégral

Où je- valeur efficace du courant total dans le circuit, I L et circuit intégré — valeurs efficaces des courants dans les branches.

En utilisant la loi d'Ohm pour déterminer les valeurs efficaces du courant dans les branches, on obtient :

Il = U / XL et Az° C = U / XC

Si le circuit est dominé par une résistance inductive, c'est-à-dire. XL Plus ▼ XC, le courant dans la bobine est inférieur au courant dans le condensateur ; par conséquent, le courant dans la section non ramifiée du circuit est de nature capacitive et le circuit dans son ensemble pour le générateur sera capacitif. A l'inverse, avec XC supérieur à XL, le courant dans le condensateur est inférieur au courant dans la bobine ; par conséquent, le courant dans la section non ramifiée du circuit est inductif, et le circuit dans son ensemble pour le générateur sera inductif.

Il ne faut pas oublier que dans les deux cas la charge est réactive, c'est-à-dire le circuit ne consomme pas la puissance du générateur.

Résonance des courants

Considérons maintenant le cas où le condensateur et la bobine connectés en parallèle se sont avérés égaux dans leur réactance, c'est-à-dire XlL = X°C.

Si, comme précédemment, nous supposons que la bobine et le condensateur n'ont pas de résistance active, alors si leurs réactions sont égales (YL = Y° C), le courant total dans la partie non ramifiée du circuit sera nul, tandis que dans les branches égales les courants circuleront avec la plus grande amplitude. Dans ce cas, le phénomène de courants de résonance se produit dans le circuit.

À la résonance actuelle, les valeurs efficaces des courants dans chaque branche, déterminées par les rapports IL = U / XL et Аz° С = U / XC seront égales entre elles, de sorte que XL = XC.

La conclusion à laquelle nous sommes parvenus peut sembler plutôt étrange à première vue. En fait, le générateur est chargé de deux résistances et il n'y a pas de courant dans la partie non ramifiée du circuit, tandis que des courants égaux et, de plus, les plus importants circulent dans les résistances elles-mêmes.

Cela s'explique par le comportement du champ magnétique de la bobine et champ électrique d'un condensateur… A la résonance des courants, comme dans résonance de tension, il y a une fluctuation d'énergie entre le champ de la bobine et le champ du condensateur. Le générateur, après avoir communiqué l'énergie au circuit, semble être isolé. Il peut être complètement éteint et le courant dans la partie dérivée du circuit sera maintenu sans générateur par l'énergie que le circuit emmagasine initialement. De plus, la tension aux bornes du circuit restera exactement la même que celle développée par le générateur.

Ainsi, lorsque l'inductance et le condensateur sont connectés en parallèle, on obtient un circuit oscillateur qui diffère de celui décrit ci-dessus uniquement en ce que le générateur qui crée les oscillations n'est pas connecté directement au circuit et le circuit est fermé. 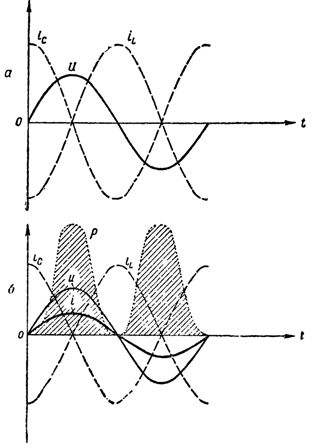Graphiques des courants, de la tension et de la puissance dans le circuit à la résonance des courants : a — la résistance active est égale à zéro, le circuit ne consomme pas d'énergie ; b — le circuit a une résistance active, un courant est apparu dans la partie non ramifiée du circuit, le circuit consomme de l'énergie

L, C et e, auxquels se produit la résonance de courant, sont déterminés, comme dans la résonance de tension (si l'on néglige la résistance active du circuit), par l'égalité :

ωL = 1 / ω° C

Donc:

ère = 1 / 2π√LC

Lres = 1 / ω2C

Pièce = 1 / ω2L

En changeant l'une de ces trois grandeurs, l'égalité Xl = X° C peut être obtenue, c'est-à-dire transformer le circuit en circuit oscillant.

Nous avons donc un circuit oscillant fermé dans lequel nous pouvons induire des oscillations électriques, c'est-à-dire courant alternatif. Et s'il n'y avait pas la résistance active que possède tout circuit oscillant, un courant alternatif pourrait y exister en permanence.La présence d'une résistance active conduit au fait que les oscillations dans le circuit s'atténuent progressivement, et pour les maintenir, une source d'énergie est nécessaire - un alternateur.

Dans les circuits de courant non sinusoïdaux, des modes de résonance sont possibles pour diverses composantes harmoniques.

Les courants de résonance sont largement utilisés dans la pratique. Le phénomène de résonance de courant est utilisé dans les filtres passe-bande comme une « pince » électrique qui retarde une certaine fréquence. Comme il existe une résistance de courant importante à la fréquence f, la chute de tension dans le circuit à la fréquence f sera maximale. Cette propriété de la boucle est appelée sélectivité, elle est utilisée dans les récepteurs radio pour isoler le signal d'une station radio particulière. Un circuit oscillant fonctionnant en mode résonnant de courants est l'un des principaux composants générateurs électroniques.