Le principe et les méthodes de détermination indirecte du facteur de puissance dans le circuit à courant alternatif

Facteur de puissance ou cosinus phi, par rapport à l'utilisateur de courant alternatif sinusoïdal, est le rapport de la consommation de puissance active P à la puissance totale S qui est fournie à cet utilisateur depuis le réseau.

Puissance totale S, dans le cas général, peut être défini comme le produit des valeurs efficaces (moyenne quadratique) du courant I et de la tension U dans le circuit considéré, et de la puissance active P — consommée de manière irréversible par l'utilisateur pour le fonctionnement du travail.

Puissance réactive Q, bien qu'il fasse partie de la puissance totale, il n'est cependant pas consommé pour effectuer un travail, mais participe uniquement à la création de champs électriques et magnétiques alternatifs dans certains éléments du circuit de l'utilisateur.

sauf mesure directe du facteur de puissance utilisation d'appareils électrodynamiques — compteurs de phase, il existe des méthodes indirectes assez logiques qui permettent de comprendre mathématiquement avec précision la valeur de cette grandeur électrique très importante qui caractérise l'utilisateur dans un circuit à courant alternatif sinusoïdal.

Regardons les données méthodes indirectes en détails, Comprenons le principe de la mesure indirecte du facteur de puissance.

Méthode voltmètre, ampèremètre et wattmètre

Wattmètre électrodynamique avec une résistance active supplémentaire dans le circuit de sa bobine mobile indique la valeur de la puissance extrêmement active consommée dans le circuit alternatif P.

Si maintenant, à l'aide d'un voltmètre et d'un ampèremètre, nous mesurons les valeurs moyennes du courant I et de la tension U agissant dans le circuit de la charge étudiée, alors en multipliant ces deux paramètres, nous n'obtiendrons que la puissance totale S .

Ensuite, le facteur de puissance (cosinus phi) d'une charge donnée peut être facilement trouvé à l'aide de la formule :

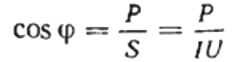
Ici, si vous le souhaitez, vous pouvez également trouver la valeur de la puissance réactive Q, la résistance totale du circuit z Loi d'Ohm, ainsi que la résistance active et réactive, simplement en construisant ou en représentant un triangle de résistance, puis en utilisant le théorème de Pythagore :

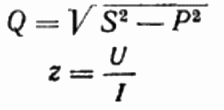
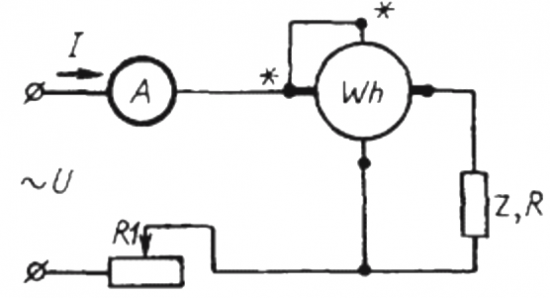
Méthode du compteur et de l'ampèremètre

Pour utiliser cette méthode, il faut monter un circuit dans lequel le plus simple est connecté en série avec la charge Z et l'ampèremètre compteur d'électricité Quoi.

Pendant une certaine durée t, de l'ordre de la minute, il faudra calculer la vitesse de rotation du disque N, qui montrera la quantité d'énergie active dépensée pendant un temps donné (c'est-à-dire en tenant compte de la facteur de puissance).

Ici : le nombre de tours du disque N, le coefficient k est la quantité d'énergie par tour, I et U sont respectivement le courant et la tension efficaces, t est le temps de comptage des tours, le cosinus phi est le facteur de puissance :

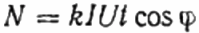
Ensuite, au lieu de l'utilisateur étudié Z, la charge active R est incluse dans le circuit via le même compteur, mais pas directement, mais via le rhéostat R1 (obtenant le même courant I que dans le premier cas, avec l'utilisateur Z). La vitesse de rotation du disque N1 est maintenue pendant un même temps t. Mais ici, puisque la charge est active, le cosinus phi (facteur de puissance) est bien égal à 1. D'où :

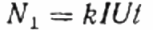
Ensuite, le rapport des tours du compteur de disque est enregistré pendant la même période de temps dans les premier et deuxième cas. Ce sera le cosinus phi, c'est-à-dire le facteur de puissance de la première charge (par rapport à une charge purement active avec le même actuel):

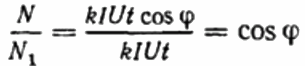
Méthode à trois ampèremètres

Pour déterminer le facteur de puissance dans un circuit de courant sinusoïdal à l'aide de trois ampèremètres, vous devez d'abord assembler le circuit suivant :

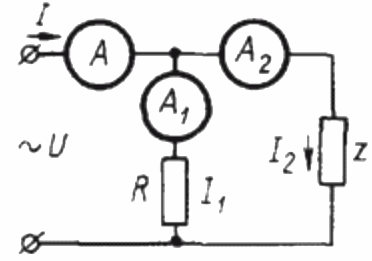
Ici Z est une charge dont le facteur de puissance est à déterminer et R est une charge purement active.

La charge R étant purement active, le courant I1 est à tout instant en phase avec la tension alternative U appliquée à cette charge Dans ce cas, le courant I est égal à la somme géométrique des courants I1 et I2. Nous allons maintenant construire à partir de cette position un diagramme vectoriel des courants :

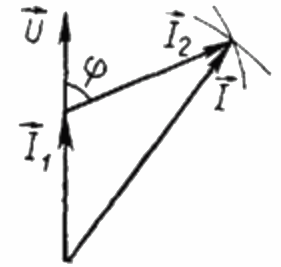
Sur le diagramme vectoriel des courants, l'angle aigu entre le courant I1 et le courant I2 est l'angle phi, dont le cosinus (en fait, la valeur du facteur de puissance) peut être trouvé à partir d'un tableau spécial de valeurs de fonctions trigonométriques ou calculées par la formule :

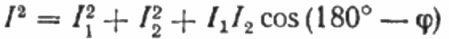
De là, nous pouvons exprimer le cosinus phi, c'est-à-dire le facteur de puissance souhaité :

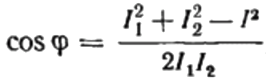
Le signe du facteur de puissance trouvé ("+" ou "-") indiquera la nature de la charge. Si le facteur de puissance (cosinus phi) est négatif, la charge est de nature capacitive. Si le facteur de puissance est une valeur positive, alors la nature de la charge est inductive.