Alimentation secteur triphasée : active, réactive, pleine

Les valeurs de la puissance active et réactive totale du circuit triphasé sont égales aux sommes des puissances active et réactive pour chacune des trois phases A, B et C, respectivement.Cette déclaration est illustrée par ce qui suit formules :

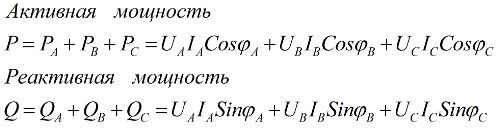
ici Ua, Ub, Uc, Ia, Ib, Ic sont les valeurs des tensions et courants de phase et φ est le déphasage.

Lorsque la charge est symétrique, c'est-à-dire dans des conditions où les puissances active et réactive de chacune des phases sont égales, pour trouver la puissance totale du circuit polyphasé, il suffit de multiplier la valeur de la puissance de phase par le nombre de phases concernées. La puissance totale est déterminée en fonction des valeurs obtenues de ses composants actifs et réactifs :

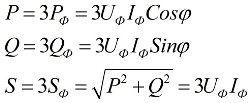
Dans les formules ci-dessus, les valeurs de phase des quantités peuvent être exprimées en fonction de leurs valeurs linéaires, qui différeront pour les schémas de connexion en étoile ou en triangle pour les utilisateurs, mais les formules de puissance seront finalement les mêmes :

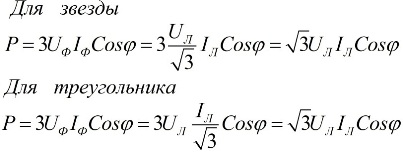
Il résulte des expressions ci-dessus que quel que soit le schéma de connexion des récepteurs d'énergie électrique, qu'il s'agisse d'un triangle ou d'une étoile, si la charge est symétrique, alors les formules pour trouver la puissance auront la même forme, à la fois pour un triangle et pour une étoile :

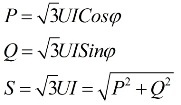
Ces formules montrent des valeurs linéaires de tension et de courant et sont écrites sans indices. Habituellement, une telle notation est trouvée, sans indices, c'est-à-dire que s'il n'y a pas d'indices, nous entendons des valeurs linéaires.

Un appareil de mesure spécial, appelé wattmètre… Ses lectures sont déterminées par la formule :

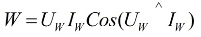
dans la formule ci-dessus, Uw et Iw sont les vecteurs de la tension appliquée à la charge et du courant qui la traverse.

La nature de la charge active et le schéma de connexion de phase peuvent être différents, par conséquent, selon les circonstances spécifiques, les schémas de connexion du wattmètre seront différents.

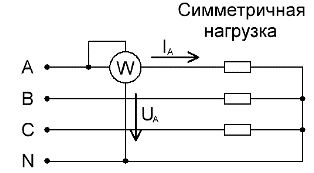
Pour les circuits triphasés chargés symétriquement, pour une mesure grossière de la puissance active totale, si une grande précision n'est pas requise, un wattmètre connecté à une seule des phases suffit. Après cela, pour obtenir la valeur de la puissance active de l'ensemble du circuit, il reste à multiplier les lectures du wattmètre par le nombre de phases :

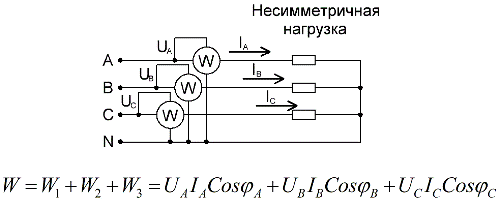
Pour un circuit à quatre fils avec un fil neutre, pour mesurer avec précision la puissance active, trois wattmètres sont nécessaires, chacun étant lu puis additionné pour obtenir une valeur de la puissance totale du circuit :

S'il n'y a pas de fil neutre dans un circuit triphasé, deux wattmètres suffisent pour mesurer la puissance totale, même si la charge est déséquilibrée.

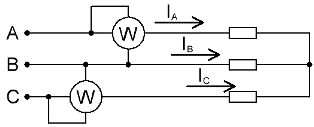
En l'absence de conducteur neutre, les courants de phase sont interconnectés selon la première loi de Kirchhoff :

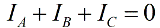
Alors la somme des lectures d'une paire de wattmètres sera égale à:

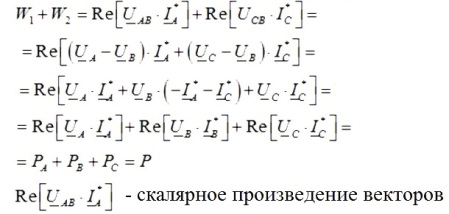
Ainsi, si vous ajoutez les lectures d'une paire de wattmètres, vous obtenez la puissance active totale dans le circuit triphasé à l'étude, et les lectures des wattmètres dépendront à la fois de la taille de la charge et de sa nature.

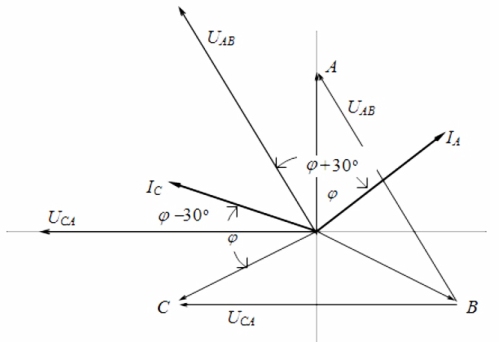
En regardant le diagramme vectoriel des courants et des tensions en relation avec une charge symétrique, on peut conclure que les lectures des wattmètres sont déterminées par les formules suivantes:

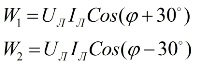
Après analyse de ces expressions, on peut comprendre qu'avec une charge purement active, lorsque φ = 0, les lectures des deux wattmètres seront égales, c'est-à-dire W1 = W2.

Avec une inductance de charge active, lorsque 0 ≤ φ ≤ 90 °, les lectures du wattmètre 1 seront inférieures à celles du wattmètre 2, c'est-à-dire W1 60 °, les lectures du wattmètre 1 seront négatives, c'est-à-dire W1 <0.

Avec une nature active-capacitive de la charge, lorsque 0 ≥ φ≥ -90 °, les lectures du wattmètre 2 seront inférieures à celles du wattmètre 1, c'est-à-dire W1> W2. À φ <-60 °, les lectures du wattmètre 2 deviendront négatives.