Qu'est-ce qu'une alimentation électrique ?

L'homme moderne rencontre constamment de l'électricité dans la vie quotidienne et au travail, utilise des appareils qui consomment du courant électrique et des appareils qui en génèrent. Lorsque vous travaillez avec eux, vous devez toujours tenir compte de leurs capacités inhérentes aux caractéristiques techniques.

L'un des principaux indicateurs de tout appareil électrique est une quantité physique telle que l'énergie électrique... Il est d'usage d'appeler l'intensité ou la vitesse de génération, de transmission ou de conversion de l'électricité en d'autres types d'énergie, par exemple, la chaleur, la lumière, mécanique.

Le transport ou le transfert de grande énergie électrique à des fins industrielles s'effectue selon lignes à haute tension.

Transformation énergie électrique est effectuée dans les postes de transformation.

La consommation d'électricité se produit dans les appareils ménagers et industriels à diverses fins. L'un de leurs types communs est lampes à incandescence de différentes puissances.

La puissance électrique des générateurs, des lignes électriques et des consommateurs dans les circuits CC et CA a la même signification physique, qui s'exprime simultanément dans des rapports différents en fonction de la forme des signaux composites. Pour définir les schémas généraux, des notions de valeurs instantanées... Ils soulignent à nouveau la dépendance du taux de transformation de l'électricité au temps.

Détermination de la puissance électrique instantanée

En génie électrique théorique, afin de dériver les relations de base entre le courant, la tension et la puissance, leurs images sous forme de valeurs instantanées, qui sont fixées à un certain moment, sont utilisées.

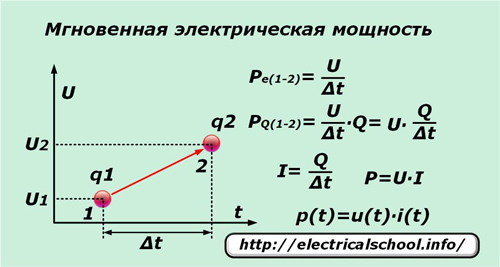
Si en un temps très court ∆t une seule charge élémentaire q sous l'influence de la tension U se déplace du point « 1 » au point « 2 », alors elle effectue un travail égal à la différence de potentiel entre ces points. En le divisant par l'intervalle de temps ∆t, on obtient l'expression de la puissance instantanée par unité de charge Pe (1-2).

Étant donné que non seulement la charge unique se déplace sous l'action de la tension appliquée, mais également toutes les charges adjacentes qui sont sous l'influence de cette force, dont le nombre est commodément représenté par le nombre Q, alors la valeur instantanée de la puissance PQ (1-2) peut être écrit pour eux.

Après avoir effectué des transformations simples, nous obtenons l'expression de la puissance P et la dépendance de sa valeur instantanée p (t) sur les composantes du produit du courant instantané i (t) et de la tension u (t).

Détermination de la puissance électrique constante

V Circuits CC l'amplitude de la chute de tension dans la section de circuit et le courant qui la traverse ne changent pas et restent stables, égaux aux valeurs instantanées.Par conséquent, la puissance de ce circuit peut être déterminée en multipliant ces valeurs ou en divisant le travail parfait A par la période de son exécution, comme indiqué dans l'image explicative.

Détermination de la puissance électrique en courant alternatif

Les lois de variation sinusoïdale des courants et des tensions transmises par les réseaux électriques imposent leur influence sur l'expression de la puissance dans de tels circuits. La puissance apparente entre en jeu ici, qui est décrite par le triangle de puissance et se compose de composants actifs et réactifs.

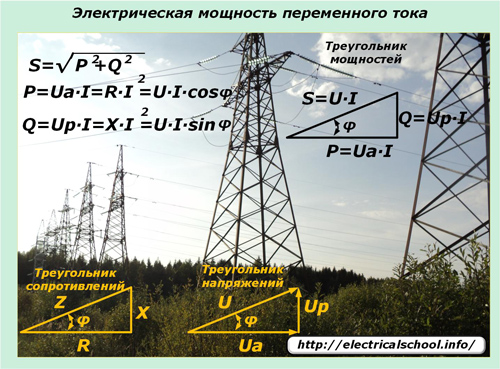
Un courant électrique sinusoïdal traversant des lignes électriques avec des types de charges mixtes dans toutes les sections ne modifie pas la forme de son harmonique.Et la chute de tension aux charges réactives se décale en phase dans une certaine direction. Les expressions de valeur de moment aident à comprendre l'effet des charges appliquées sur le changement de puissance dans le circuit et sa direction.

Dans le même temps, faites immédiatement attention au fait que la direction du flux de courant du générateur au consommateur et la puissance transmise à travers le circuit créé sont des choses complètement différentes, qui dans certains cas peuvent non seulement ne pas coïncider, mais aussi être dirigés dans des directions opposées.

Considérez ces relations dans leur manifestation idéale et pure pour différents types de charges :

• actif;

• capacitif ;

• inductif.

Dissipation de puissance de charge active

Nous supposerons que le générateur produit une tension sinusoïdale idéale u qui est appliquée à la résistance purement active du circuit. L'ampèremètre A et le voltmètre V mesurent le courant I et la tension U à chaque instant t.

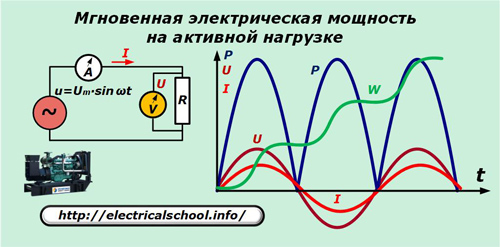
Le graphique montre que les sinusoïdes du courant et la chute de tension aux bornes de la résistance active correspondent en fréquence et en phase, faisant les mêmes oscillations. La force exprimée par leur produit oscille à deux fois la fréquence et reste toujours positive.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Si l'on passe à l'expression tension de fonctionnement, alors on obtient : p = P ∙ (1-cos2ωt).

On intégrera alors la puissance sur la période d'une oscillation T et on pourra remarquer que le gain d'énergie ∆W pendant cet intervalle augmente. Au fil du temps, la résistance continue de consommer de nouvelles portions d'électricité, comme le montre le graphique.

Avec les charges réactives, les caractéristiques de consommation d'énergie sont différentes, elles ont une forme différente.

Dissipation de puissance capacitive

Dans le circuit électrique du générateur, remplacez l'élément résistif par un condensateur de capacité C.

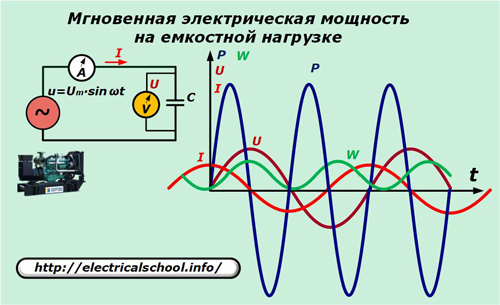
La relation entre le courant et la chute de tension dans la capacité s'exprime par le rapport : I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Nous multiplions les valeurs des expressions instantanées du courant avec la tension et obtenons la valeur de la puissance consommée par la charge capacitive.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Ici, vous pouvez voir que la puissance fluctue autour de zéro à deux fois la fréquence de la tension appliquée. Sa valeur totale pour la période harmonique, ainsi que le gain d'énergie, est nulle.

Cela signifie que l'énergie se déplace le long du circuit fermé du circuit dans les deux sens, mais ne fonctionne pas.Un tel fait s'explique par le fait que lorsque la tension de la source augmente en valeur absolue, la puissance est positive et le flux d'énergie à travers le circuit est dirigé vers le conteneur, où l'énergie est accumulée.

Une fois que la tension est passée à la section harmonique descendante, l'énergie est renvoyée du condensateur au circuit vers la source. Aucun travail utile n'est effectué dans l'un ou l'autre processus.

Dissipation de puissance dans une charge inductive

Maintenant, dans le circuit d'alimentation, remplacez le condensateur par l'inductance L.

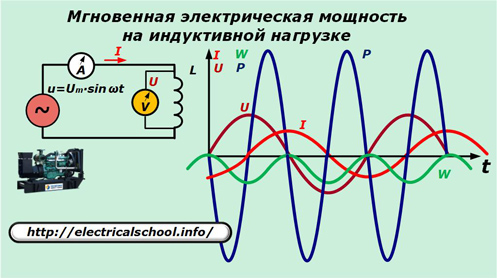
Ici, le courant traversant l'inductance est exprimé par le rapport :

je = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Ensuite on obtient

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ÜL) ∙ sin2ωt = -U2/ (2ÜL) ∙ sin2ωt.

Les expressions résultantes nous permettent de voir la nature du changement de direction de la puissance et de l'augmentation d'énergie sur l'inductance, qui effectue les mêmes oscillations inutiles pour faire le travail, que sur la capacité.

La puissance libérée dans les charges réactives est appelée composante réactive. Dans des conditions idéales, lorsque les fils de connexion n'ont pas de résistance active, cela semble inoffensif et ne cause aucun dommage. Mais dans des conditions de puissance réelles, les transitoires périodiques et les fluctuations de puissance réactive provoquent un échauffement de tous les éléments actifs, y compris les fils de connexion, pour lesquels une certaine énergie est consommée et la valeur de la pleine puissance appliquée de la source diminue.

La principale différence entre la composante réactive de la puissance est qu'elle n'effectue aucun travail utile, mais entraîne des pertes d'énergie électrique et des charges excessives sur les équipements, qui sont particulièrement dangereuses dans les situations critiques.

Pour ces raisons, pour éliminer l'influence de la puissance réactive, en particulier systèmes techniques pour sa compensation.

Distribution de puissance à charge mixte

A titre d'exemple, nous utilisons la charge d'un générateur avec une caractéristique capacitive active.

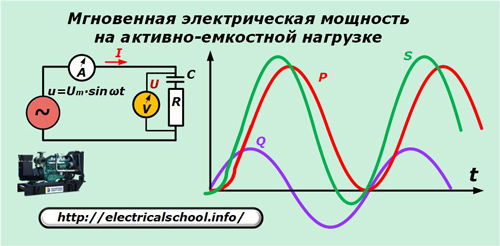
Pour simplifier l'image, les sinusoïdes des courants et des tensions ne sont pas représentées dans le graphique donné, mais il convient de garder à l'esprit qu'avec une nature capacitive active de la charge, le vecteur courant est en avance sur la tension.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Après transformations on obtient : p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Ces deux termes dans la dernière expression sont les composantes active et réactive de la puissance apparente instantanée. Seul le premier d'entre eux fait un travail utile.

Outils de mesure de puissance

Pour analyser la consommation d'électricité et la calculer, on utilise des appareils de mesure, qui ont longtemps été appelés "Compteurs"… Leur travail est basé sur la mesure des valeurs efficaces du courant et de la tension et sur leur multiplication automatique avec une sortie d'informations.

Les compteurs affichent la consommation d'énergie en comptant le temps de fonctionnement des appareils électriques de manière incrémentale à partir du moment où le compteur est allumé en charge.

Pour mesurer la composante active de la puissance dans les circuits AC, wattmètres, et réactif - varmètres. Ils ont différentes désignations d'unité :

• watt (W, W);

• var (var, var, var).

Pour déterminer la consommation d'énergie totale, il est nécessaire de calculer sa valeur à l'aide de la formule du triangle de puissance basée sur les lectures du wattmètre et du varmètre. Il est exprimé dans ses propres unités - volt-ampères.

Les désignations acceptées des unités de chacun aident les électriciens à juger non seulement de sa valeur, mais également de la nature du composant de puissance.