Triangles de tensions, résistances et puissances

Quiconque a une idée des diagrammes vectoriels remarquera facilement qu'on y distingue très clairement un triangle de tension à angle droit, dont chaque côté reflète: la tension totale du circuit, la tension de la résistance active et la tension sur la réactance.

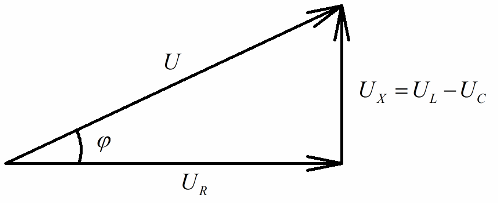
Conformément au théorème de Pythagore, la relation entre ces tensions (entre la tension totale du circuit et la tension de ses sections) ressemblera à ceci :

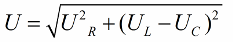
Si l'étape suivante consiste à diviser les valeurs de ces tensions par le courant (le courant circule également dans toutes les sections du circuit série), alors par Loi d'Ohm nous obtenons les valeurs de résistance, c'est-à-dire que nous pouvons maintenant parler d'un triangle rectangle de résistances :

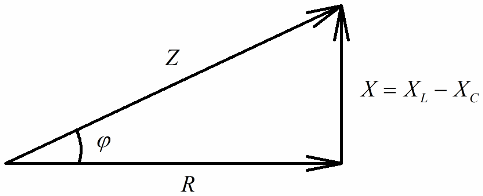
De manière similaire (comme dans le cas des tensions), en utilisant le théorème de Pythagore, il est possible d'établir une relation entre l'impédance du circuit et les réactances. La relation s'exprimera par la formule suivante :

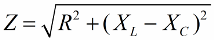
Ensuite, nous multiplions les valeurs de résistance par le courant, en fait nous allons augmenter chaque côté du triangle rectangle d'un certain nombre de fois. On obtient alors un triangle rectangle de capacités :

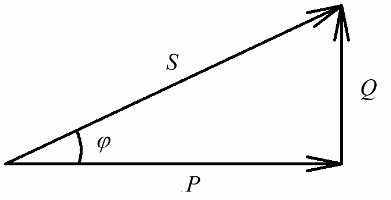
La puissance active libérée au niveau de la résistance active du circuit associée à la conversion irréversible de l'énergie électrique (en chaleur, dans l'exécution des travaux dans l'installation) sera clairement liée à la puissance réactive impliquée dans la conversion réversible de l'énergie (la création des champs magnétiques et électriques dans les bobines et les condensateurs) et à pleine puissance fournie à l'installation électrique.

La puissance active est mesurée en watts (W), la puissance réactive — en varis (VAR — volt-ampère réactif), totale — en VA (volt-ampère).

D'après le théorème de Pythagore, on a le droit d'écrire :

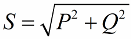
Faisons maintenant attention au fait que dans le triangle de puissance, il existe un angle phi, dont le cosinus est facile à déterminer principalement par la puissance active et la puissance apparente. Le cosinus de cet angle (cos phi) appelé facteur de puissance. Il montre quelle part de la puissance totale est prise en compte lors d'un travail utile dans une installation électrique et n'est pas renvoyée au réseau.

De toute évidence, un facteur de puissance plus élevé (maximum un) indique un rendement de conversion plus élevé de l'énergie fournie à la centrale pour son fonctionnement. Si le facteur de puissance est de 1, alors toute l'énergie fournie est utilisée pour effectuer le travail.

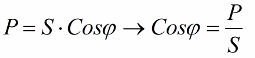
Les ratios obtenus permettent d'exprimer la consommation de courant de l'installation en termes de facteur de puissance, de puissance active et de tension réseau :

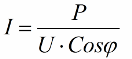
Ainsi, plus le cosinus phi est petit, plus le réseau a besoin de courant pour effectuer un certain travail. En pratique, ce facteur (courant maximal du réseau) limite la capacité de transmission de la ligne de transmission et donc, plus le facteur de puissance est faible, plus la charge de la ligne est importante et plus la bande passante utile est faible (le cosinus phi faible entraîne une restriction). Les pertes Joule dans les lignes électriques avec un cosinus phi décroissant peuvent être vues à partir de la formule suivante :

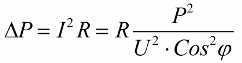
Sur la résistance active R de la ligne de transmission, les pertes augmentent d'autant plus que le courant I est élevé, même s'il est réactif à la charge. Par conséquent, on peut dire qu'avec un faible facteur de puissance, le coût de transport de l'électricité augmente simplement. Cela signifie que l'augmentation du cosinus phi est une tâche économique nationale importante.

Il est souhaitable que la composante réactive de la puissance totale soit proche de 0. Pour cela, il serait bon de toujours utiliser les moteurs électriques et les transformateurs à pleine charge et de les éteindre en fin d'utilisation pour qu'ils ne tournent pas au ralenti. A vide, les moteurs et les transformateurs ont un facteur de puissance très faible. Une façon d'augmenter le cosinus phi chez les utilisateurs consiste à utiliser batteries de condensateurs et compensateurs synchrones.